
ijͬѧ�á����λ��塷�о������ߵ����ʣ������λ��塷����������ij������E��y
2=2px���������������⻭һ����S��������S�����꣨x
S��y
S������ͼ��
�����϶���S�����ֵ�x
S=4ʱ��y
S=4������������E�ķ��̣�
������������E�Ķ���ΪA������ΪF������ֱ��SF��������E�ڲ�ͬ����S��T������ֱ��AS��AT�ֱ�����M��N���㣬����ֱ��MT��NS�����۲�ã�����������E�����������϶���S������MT��NS������֤����һ���ۣ�
����Ϊ��һ���о���������E�����ʣ�ijͬѧ����������ij��ԣ��ڣ����У��ѡ�����F���ı�Ϊ����������G��g��0����g��0�����������������䣬���֡�MT��NS����ƽ�С����Ƿ�����ʵ����ģ����е�����������ʹ�����С�MT��NS��������������ԣ���д����Ӧ����ȷ���⣻����˵�����ɣ�

 ijͬѧ�á����λ��塷�о������ߵ����ʣ������λ��塷����������ij������E��y2=2px���������������⻭һ����S��������S�����꣨xS��yS������ͼ��
ijͬѧ�á����λ��塷�о������ߵ����ʣ������λ��塷����������ij������E��y2=2px���������������⻭һ����S��������S�����꣨xS��yS������ͼ��

 ��У����ϵ�д�
��У����ϵ�д�
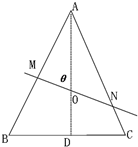 ��ͼ���ȱߡ�ABC�У�AB=3��OΪ���ģ���O��ֱ�߽�AB��M����AC��N�����AOM=�ȣ�0�ܦȡ�120�㣩�����ȷֱ�Ϊ��ֵʱ��
��ͼ���ȱߡ�ABC�У�AB=3��OΪ���ģ���O��ֱ�߽�AB��M����AC��N�����AOM=�ȣ�0�ܦȡ�120�㣩�����ȷֱ�Ϊ��ֵʱ��