
| A. | 1 | B. | -1 | C. | 2 | D. | -2 |
分析 在所给的等式中,分别令x=1、x=-1,可得2个式子,再把这2个式子相乘、变形可得要求式子的值.
解答 解:∵${(2x+\sqrt{3})^{21}}={a_0}+{a_1}x+{a_2}{x^2}+…+{a_{21}}{x^{21}}$,
∴令x=1,可得a0+a1+a2+a3+…+a21=${(2+\sqrt{3})}^{21}$ ①,
令x=-1,可得得a0-a1+a2-a3+…+a21=${(-2+\sqrt{3})}^{21}$ ②,
①乘以②可得 ${({a_0}+{a_2}+{a_4}+…+{a_0})^2}$-${{(a}_{1}{+a}_{3}+…{+a}_{21})}^{2}$=-1,
那么${({a_1}+{a_3}+{a_5}+…+{a_{21}})^2}-$${({a_0}+{a_2}+{a_4}+…+{a_0})^2}$=1,
故选:A.
点评 本题主要考查二项式定理的应用,是给变量赋值的问题,关键是根据要求的结果,选择合适的数值代入,属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
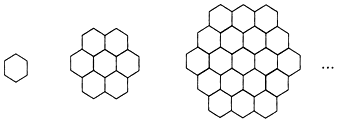 单个蜂巢可以近似地看作是一个正六边形,如图为一组蜂巢的截面图.其中第一个图有1个蜂巢,第二个图有7个蜂巢,第三个图有19个蜂巢,按此规律,以f(n)表示第n幅图的蜂巢总数.则f(4)=________;f(n)=________( )
单个蜂巢可以近似地看作是一个正六边形,如图为一组蜂巢的截面图.其中第一个图有1个蜂巢,第二个图有7个蜂巢,第三个图有19个蜂巢,按此规律,以f(n)表示第n幅图的蜂巢总数.则f(4)=________;f(n)=________( )| A. | 37 3n2-3n+1 | B. | 38 3n2-3n+2 | C. | 36 3n2-3n | D. | 35 3n2-3n-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{{\sqrt{3}}}{2}$ | B. | $-\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 必要不充分条件 | B. | 充分不必要条件 | ||
| C. | 充分必要条件 | D. | 即不充分也不必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com