
分析 (1)根据指数幂的运算法则即可求[g(x)]2-[f(x)]2的值;
(2)根据条件f(x)•f(y)=8,g(x)•g(y)=4,利用方程组即可求$\frac{f(x+y)}{f(x-y)}$的值;
(3)结合一元二次方程即可求ax及ay的值.
解答 解:(1)∵f(x)=ax+a-x,g(x)=ax-a-x,
∴[g(x)]2-[f(x)]2=(ax-a-x)2-(ax+a-x)2=a2x-2+a-2x-a2x-2-a-2x=-4.
(2)∵f(x)•f(y)=8,
∴f(x)•f(y)=(ax+a-x)(ay+a-y)=8,
即ax+y+a-x+y+ax-y+a-x-y=8 ①
∵g(x)•g(y)=4,
∴g(x)•g(y)=(ax-a-x)•(ay-a-y)=4.
即ax+y-ax-y-a-x+y+a-x-y=4,②
①+②,得 2(ax+y+a-x-y)=12,
∴ax+y+a-x-y=6,
即f(x+y)=6,
①-②,得2(ax-y+a-x+y)=4.
∴ax-y+a-x+y=2.即f(x-y)=2.
则$\frac{f(x+y)}{f(x-y)}$=$\frac{6}{2}=3$.
(3)∵ax+y+a-x-y=6,
∴ax+y+$\frac{1}{{a}^{x+y}}$=6,
即(ax+y)2-6(ax+y)+1=0,
即ax+y=3+2$\sqrt{2}$或ax+y=3-2$\sqrt{2}$,
∵ax-y+a-x+y=2.
∴(ax-y)2-2(ax-y)+1=0
ax-y=1,即x-y=0,则x=y,
即a2x=3+2$\sqrt{2}$=(3+$\sqrt{2}$)2或a2x=3-2$\sqrt{2}$=(3-$\sqrt{2}$)2,
∴则ax=3+$\sqrt{2}$或ax=3-$\sqrt{2}$,
即ay=3+$\sqrt{2}$或ay=3-$\sqrt{2}$.
点评 本题主要考查指数幂的运算法则,考查学生的计算能力.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
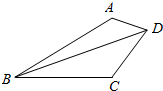 如图,在四边形ABCD中,AB=4,BC=3,CD=2,DA=1,四边形的四个角分别记为A,B,C,D.
如图,在四边形ABCD中,AB=4,BC=3,CD=2,DA=1,四边形的四个角分别记为A,B,C,D.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | -8 | C. | -2 | D. | 8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com