练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    19．等差数列{an}的前n项和为Sn，已知S3=a2+10a1，a5=34，则a1=（　　）
    A．1B．2C．3D．4

    分析 利用等差数列通项公式与求和公式即可得出．

    解答 解：设等差数列{an}的公差为d，∵S3=a2+10a1，a5=34，
    ∴3a1+3d=11a1+d，a1+4d=34，
    则a1=2．
    故选：B．

    点评 本题考查了等差数列的通项公式、求和公式，考查了推理能力与计算能力，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    9．在等比数列{an}中，Sn是其前n项和，若a3=3且2Sn+3Sn+2=5Sn+1，则数列{an}的通项公式为an=$3×（\frac{2}{3}）^{n-3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．将一个气球的半径扩大1倍，它的体积扩大到原来的（　　）倍．
    A．1B．2C．4D．8

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．电视传媒公司为了了解某地区电视观众对耨泪体育节目的收视情况，随机抽取了100名观众进行调查，下面是根据调查得到的2×2列联表：
    非体育迷体育迷总计
    男301545
    女451055
    总计7525100
    问：在犯错误的概率不超过0.10的前提下，是否可以认为“体育迷”与性别有关．
    P（K2≥k0）0.150.100.050.0250.0100.0050.001
    k02.0722.7063.8415.0246.6357.87910.828
    ${K^2}=\frac{{n{{（ab-bc）}^2}}}{（a+b）（b+c）（a+c）（b+d）}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．以下命题中：
    ①从匀速传递的产品流水线上，质检员每10分钟从中抽取一件产品进行某项指标检测，这样的抽样是分层抽样；
    ②两个随机变量的线性相关性越强，相关系数的绝对值越接近于1；
    ③已知随机变量ξ+η=8，若ξ～B（10，0.6），则Eη，Dη分别是2和2.4；
    ④设随机变量ξ服从正态分布N（3，7），若P（ξ＞a+2）=P（ξ＜a-2），则a=2；
    其中真命题的个数为（　　）
    A．1B．2C．3D．4

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．已知椭圆的中心在原点，焦点在x轴上，离心率为$\frac{\sqrt{3}}{2}$，且经过点M（4，1）．直线l：y=x+m交椭圆于A，B两不同的点．
    （1）求椭圆方程；
    （2）若直线l与椭圆有两个不同的交点，求m的取值范围；  
    （3）若直线l不过点M，求证：直线MA，MB与x轴围成等腰三角形．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．已知函数f（x）=2x2-ax+5在区间[1，+∞）上是单调递增函数，则实数a的取值范围是（　　）
    A．（-∞，4]B．（-∞，4）C．[4，+∞）D．（4，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

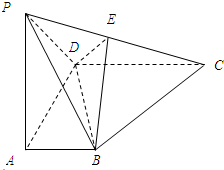    8．如图，四棱锥P-ABCD底面为一直角梯形，AB⊥AD，CD⊥AD，CD=2AB，PA⊥面ABCD，E为PC中点
    （Ⅰ）求证：平面PDC⊥平面PAD
    （Ⅱ）求证：BE∥平面PAD
    （Ⅲ） 假定PA=AD=CD，求二面角E-BD-C的正切值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．如图所示：O、A、B是平面上的三点，设向量$\overrightarrow{OA}$=$\overrightarrow{a}$，$\overrightarrow{OB}$=$\overrightarrow{b}$，且|$\overrightarrow{a}$|=3，|$\overrightarrow{b}$|=2在平面AOB上，若P为线段AB的中垂线上任意一点，则$\overrightarrow{OP}$•（$\overrightarrow{a}$-$\overrightarrow{b}$）的值是（　　）
    A．$\frac{5}{2}$B．5C．3D．$\frac{3}{2}$

    查看答案和解析>>

    同步练习册答案