
分析 (1)利用函数的奇偶性的定义,判断证明即可.
(2)求出函数的导数,判断函数的单调性,求出函数的最值即可.
(3)利用函数的导数,求出导数的最小值即可证明结果.
解答 解:(1)∵$f(x)={e^x}-{e^{-x}}={e^x}-\frac{1}{e^x}$,ex>0,
函数y=f(x)的定义域为实数R关于原点对称 (2分)
又∵f(-x)=e-x-ex=-(ex-e-x)=-f(x)
∴函数y=f(x)为奇函数.(4分)
(2)f(x)的导数$f'(x)=({e^x}-\frac{1}{e^x})'={e^x}+{e^{-x}}$>0恒成立.所以函数y=f(x)定义域上 为单调增函数(也可用定义证明) ( 8分)
所以函数y=f(x)在区间[2,3]上也单调递增;函数y=f(x)在x=3处取得最大值,且最大值为$f(3)={e^3}-{e^{-3}}=\frac{{{e^6}-1}}{e^3}$
在x=2处取得最小值,且最小值为$f(2)={e^2}-{e^{-2}}=\frac{{{e^4}-1}}{e^2}$( 12分)
(3)由于f(x)的导数$f'(x)=({e^x}-\frac{1}{e^x})'={e^x}+{e^{-x}}$$≥2\sqrt{{e^x}•{e^{-x}}}=2$,故f′(x)≥2.
(当且仅当x=0时,等号成立). (16分)
点评 本题考查函数的导数的应用,函数的最值的求法,考查分析问题解决问题的能力.


科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{2}$ | B. | 0 | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 60° | C. | 120° | D. | 150° |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 由于当前学生课业负担重,造成青少年视力普遍下降,现从某高中随机抽取16名学生,经校医用视力表检查得到每个学生的视力状况的茎叶图(以小数点前的一位数字为茎,小数点后的一位数字为叶)如图:请指出这组数据的中位数为4.75.
由于当前学生课业负担重,造成青少年视力普遍下降,现从某高中随机抽取16名学生,经校医用视力表检查得到每个学生的视力状况的茎叶图(以小数点前的一位数字为茎,小数点后的一位数字为叶)如图:请指出这组数据的中位数为4.75.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
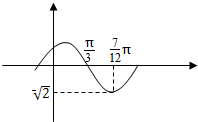 函数f(x)=Asin(ωx+φ)(A>0,ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示,
函数f(x)=Asin(ωx+φ)(A>0,ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com