Question

【题目】某水泥厂销售工作人员根据以往该厂的销售情况，绘制了该厂日销售量的频率分布直方图，如图所示：将日销售量落入各组的频率视为概率，并假设每天的销售量相互独立．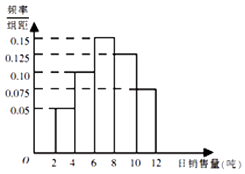
（1）求未来3天内，连续2天日销售量不低于8吨，另一天日销售量低于8吨的概率；
（2）用X表示未来3天内日销售量不低于8吨的天数，求随机变量X的分布列及数学期望．

Answer 1

【答案】
（1）解：由频率分布直方图可知，

日销售量不低于8吨的频率为：2×（0.125+0.075）=0.4，

记未来3天内，第i天日销售量不低于8吨为事件A1（i=1，2，3），

则P（A1）=0.4，

未来3天内，连续2天日销售不低于8吨，

另一天日销量低于8吨包含两个互斥事件 和 ，

则未来3天内，连续2天日销售量不低于8吨，另一天日销售量低于8吨的概率：

=0.4×0.4×（1﹣0.4）+（1﹣0.4）×0.4×0.4=0.192

（2）解：X的可能取值为0，1，2，3，且X～B（3，0.4）

P（X=0）=（1﹣0.4）3=0.216，

，

，

P（X=3）=0.43=0.064，

∴X的分布列为：

X	0	1	2	3
P	0.216	0.432	0.288	0.064

E（X）=3×0.4=1.2

【解析】（Ⅰ）由频率分布直方图求出日销售量不低于8吨的频率为0.4，记未来3天内，第i天日销售量不低于8吨为事件A1（i=1，2，3），未来3天内，连续2天日销售不低于8吨，另一天日销量低于8吨包含两个互斥事件 和 ，由此能求出未来3天内，连续2天日销售量不低于8吨，另一天日销售量低于8吨的概率．（Ⅱ）X的可能取值为0，1，2，3，且X～B（3，0.4），由此能求出X的分布列和E（X）．