
分析 (1)当m=0时,f(x)=ex-2x.f'(x)=ex-2,根据导数的符号确定单调性;
(2)由f'(x)=ex-2mx-2,$f''(x)={e^x}-2m>{e^x}-2•\frac{e-2}{2}={e^x}-(e-2)$.可证得f'(x)单调递增.
又$f'(0)=1-2=-1<0,f'(1)=e-2m-2>e-2×({\frac{e}{2}-1})-2=0$,即存在唯一的x0∈(0,1),使得f'(x0)=0,即${e^{x_0}}-2m{x_0}-2=0$,得$f{(x)_{min}}={e^{x_0}}-\frac{{{e^{x_0}}-2}}{{2{x_0}}}x_0^2-2{x_0}={e^{x_0}}-\frac{1}{2}{x_0}{e^{x_0}}-{x_0}$.利用导数可得$g(x)>g(1)=\frac{e}{2}-1$,即可得证.
解答 解:(1)当m=0时,f(x)=ex-2x.f'(x)=ex-2,令f'(x)>0,得x>ln2.
易知f(x)在(-∞,ln2)上单调递减,f(x)在(ln2,+∞)上单调递增.
(2)证明:f'(x)=ex-2mx-2,$f''(x)={e^x}-2m>{e^x}-2•\frac{e-2}{2}={e^x}-(e-2)$.
当x∈[0,+∞)时,ex≥1>e-2,故f''(x)>0,故f'(x)单调递增.
又$f'(0)=1-2=-1<0,f'(1)=e-2m-2>e-2×({\frac{e}{2}-1})-2=0$,
故存在唯一的x0∈(0,1),使得f'(x0)=0,即${e^{x_0}}-2m{x_0}-2=0$,
且当x∈(0,x0)时,f'(x)<0,故f(x)单调递减,
当x∈(x0,+∞)时,f'(x)>0,故f(x)单调递增.
故$f{(x)_{min}}=f({x_0})={e^{x_0}}-mx_0^2-2{x_0}$.
因为x=x0是方程${e^{x_0}}-2m{x_0}-2=0$的根,故$m=\frac{{{e^{x_0}}-2}}{{2{x_0}}}$.
故$f{(x)_{min}}={e^{x_0}}-\frac{{{e^{x_0}}-2}}{{2{x_0}}}x_0^2-2{x_0}={e^{x_0}}-\frac{1}{2}{x_0}{e^{x_0}}-{x_0}$.
令$g(x)={e^x}-\frac{1}{2}x{e^x}-x,x∈(0,\;1)$,$g'(x)=\frac{1}{2}{e^x}-\frac{1}{2}x{e^x}-1$,$g''(x)=-\frac{1}{2}x{e^x}<0$.
故g'(x)在(0,1)上单调递减,故$g'(x)<g'(0)=-\frac{1}{2}<0$,
故g(x)在(0,1)上单调递减,
∴$g(x)>g(1)=\frac{e}{2}-1$,故$f(x)>\frac{e}{2}-1$.
点评 本题考查了导数的综合应用,考查了函数的单调性、最值问题,转化思想,属于难题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 0.48 | B. | 0.40 | C. | 0.64 | D. | 0.75 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
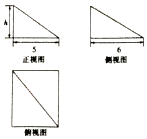
| A. | 8π | B. | 24π | C. | 48π | D. | 64π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [2,+∞) | B. | [4,+∞) | C. | [8,+∞) | D. | (0,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com