
| A. | (-∞,6) | B. | (-∞,6] | C. | [6,+∞) | D. | (6,+∞) |
分析 当x>0时,不等式x2-mx+9>0恒成立?m<(x+$\frac{9}{x}$)min,利用基本不等式可求得(x+$\frac{9}{x}$)min=6,从而可得实数m的取值范围.
解答 解:当x>0时,不等式x2-mx+9>0恒成立?当x>0时,不等式m<x+$\frac{9}{x}$恒成立?m<(x+$\frac{9}{x}$)min,
当x>0时,x+$\frac{9}{x}$≥2$\sqrt{x•\frac{9}{x}}$=6(当且仅当x=3时取“=”),
因此(x+$\frac{9}{x}$)min=6,
所以m<6,
故选:A.
点评 本题考查函数恒成立问题,分离参数m是关键,考查等价转化思想与基本不等式的应用,属于中档题.


科目:高中数学 来源: 题型:填空题
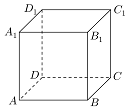 如图,ABCD-A1B1C1D1是棱长为1的正方体,任作平面α与对角线AC1垂直,使得α与正方体的每个面都有公共点,这样得到的截面多边形的面积为S,周长为l的范围分别是[$\frac{\sqrt{3}}{2}$,$\frac{3\sqrt{3}}{4}$]、{3$\sqrt{2}$}(用集合表示)
如图,ABCD-A1B1C1D1是棱长为1的正方体,任作平面α与对角线AC1垂直,使得α与正方体的每个面都有公共点,这样得到的截面多边形的面积为S,周长为l的范围分别是[$\frac{\sqrt{3}}{2}$,$\frac{3\sqrt{3}}{4}$]、{3$\sqrt{2}$}(用集合表示)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 9 | C. | 10 | D. | 11 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 一条射线 | B. | 两条射线 | C. | 一条直线 | D. | 两条直线 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com