
分析 (Ⅰ)f(x)=$\frac{|3x+2|-|1-2x|}{|x+3|}$≤$\frac{|3x+2+1-2x|}{|x+3|}$=1即可,
(Ⅱ)由2(a+b+c)+1≥2(a+b+a2+b2)+1≥2[a+b+$\frac{(a+b)^{2}}{2}$]+1=(a+b+1)2≥0,即可判定.
解答 解:(Ⅰ)f(x)=$\frac{|3x+2|-|1-2x|}{|x+3|}$≤$\frac{|3x+2+1-2x|}{|x+3|}$=1,
当且仅当x$≤-\frac{2}{3}$或x$≥\frac{1}{2}$时,等号成立,∴最大值M=1.
(Ⅱ)2(a+b+c)+1≥2(a+b+a2+b2)+1≥2[a+b+$\frac{(a+b)^{2}}{2}$]+1=(a+b+1)2≥0,
当且仅当a=b=-$\frac{1}{2}$,c=$\frac{1}{2}$时取等,
所以存在满足a2+b2≤c≤M的实数a,b,c使得2(a+b+c)+1≥0.
点评 本题考查了绝对值不等式的性质,基本不等式的应用,属于中档题.


 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源: 题型:填空题
| 7806 6572 0802 6314 2947 1821 9800 3204 9234 4935 3623 4869 6938 7481 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| p(k2≥k0) | 0.050 | 0.010 | 0.001 |
| k0 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
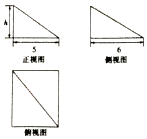
| A. | 8π | B. | 24π | C. | 48π | D. | 64π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①④ | B. | ②③ | C. | ①②③ | D. | ①③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [2,+∞) | B. | [4,+∞) | C. | [8,+∞) | D. | (0,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{100π}{3}$ | B. | 64π | C. | 100π | D. | $\frac{500π}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com