
| p��k2��k0�� | 0.050 | 0.010 | 0.001 |
| k0 | 3.841 | 6.635 | 10.828 |
���� ��1�����������������������
��2������K2�Ĺ۲�ֵ�������ٽ�ֵ���ɵó����ۣ�
��� �⣺��1�������������ݵõ���������
| ���з�ʽ �Ա� | ������ | �˶� | �ϼ� |
| Ů | 43 | 27 | 70 |
| �� | 21 | 33 | 54 |
| �ϼ� | 64 | 60 | 124 |
���� ���⿼���˶����Լ����Ӧ�����⣬�ǻ����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
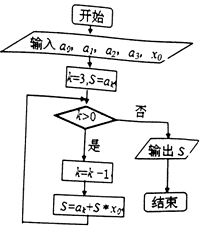 �ؾ������ҹ�����ʱ������ѧ�ң����������������¡����ҹ�13������ѧ�ɾ͵Ĵ���֮һ����ͼ���ؾ����㷨��һ�������ͼ���������SΪ��������
�ؾ������ҹ�����ʱ������ѧ�ң����������������¡����ҹ�13������ѧ�ɾ͵Ĵ���֮һ����ͼ���ؾ����㷨��һ�������ͼ���������SΪ��������| A�� | a1+x0��a3+x0��a0+a2x0������ֵ | B�� | a3+x0��a2+x0��a1+a0x0������ֵ | ||
| C�� | a0+x0��a1+x0��a2+a3x0������ֵ | D�� | a2+x0��a0+x0��a3+a1x0������ֵ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��$\frac{3}{4}$��+�ޣ� | B�� | [1��+�ޣ� | C�� | ��$\frac{3}{4}$��1] | D�� | {1} |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
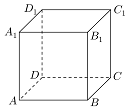 ��ͼ��ABCD-A1B1C1D1���ⳤΪ1�������壬����ƽ�����Խ���AC1��ֱ��ʹ�æ����������ÿ���涼�й����㣬�����õ��Ľ������ε����ΪS���ܳ�Ϊl�ķ�Χ�ֱ���[$\frac{\sqrt{3}}{2}$��$\frac{3\sqrt{3}}{4}$]��{3$\sqrt{2}$}���ü��ϱ�ʾ��
��ͼ��ABCD-A1B1C1D1���ⳤΪ1�������壬����ƽ�����Խ���AC1��ֱ��ʹ�æ����������ÿ���涼�й����㣬�����õ��Ľ������ε����ΪS���ܳ�Ϊl�ķ�Χ�ֱ���[$\frac{\sqrt{3}}{2}$��$\frac{3\sqrt{3}}{4}$]��{3$\sqrt{2}$}���ü��ϱ�ʾ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
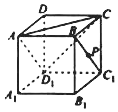 ��������ABCD-A1B1C1D1�У���ͼ������֪��P��ֱ��BC1���˶����������ĸ����⣺
��������ABCD-A1B1C1D1�У���ͼ������֪��P��ֱ��BC1���˶����������ĸ����⣺�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | p��q | B�� | �Vp�ģ��Vq�� | C�� | p��q | D�� | �Vp��q |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | һ������ | B�� | �������� | C�� | һ��ֱ�� | D�� | ����ֱ�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com