
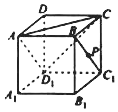
 在正方体ABCD-A1B1C1D1中(如图),已知点P在直线BC1上运动.则下列四个命题:
在正方体ABCD-A1B1C1D1中(如图),已知点P在直线BC1上运动.则下列四个命题:分析 利用体积公式判断①,利用向量计算夹角判断②,根据二面角的定义判断③,利用全等判断④.
解答 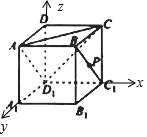 解:对于①,显然三棱锥A-D1BC体积与P点位置无关,故①正确;
解:对于①,显然三棱锥A-D1BC体积与P点位置无关,故①正确;
对于②,以D1为坐标原点,建立如图所示的空间坐标系,设正方体边长为1,则$\overrightarrow{D{B}_{1}}$=(1,1,-1)为平面ACD1的法向量,
而$\overrightarrow{AB}$=(1,0,0),$\overrightarrow{A{C}_{1}}$=(1,-1,-1),
∴cos<$\overrightarrow{AB},\overrightarrow{D{B}_{1}}$>=$\frac{1}{\sqrt{3}}$=$\frac{\sqrt{3}}{3}$,cos<$\overrightarrow{A{C}_{1}}$,$\overrightarrow{D{B}_{1}}$>=$\frac{1}{\sqrt{3}×\sqrt{3}}$=$\frac{1}{3}$,
∴AB,AC1与平面ACD1所成的角不相等,即当p在直线BC1上运动时,AP平面ACD1所成的角会发生变化,故②错误;
对于③,当P位置变化时,平面PAD1的位置不发生变化,故二面角P-AD1-C的大小不变,故③正确;
对于④,设Q为直线A1D1上任意一点,则Rt△QDD1≌Rt△QC1D1,
∴QD=QC1,
∴M的轨迹为直线AD1,故④正确.
故答案为:①③④.
点评 本题考查了棱柱的结构特征,空间线面位置关系的判断,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | (-1,1) | B. | $(0,\frac{2}{3})$ | C. | $(\frac{1}{3},1)$ | D. | (0,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在正三棱锥A-BCD中,AB=$\sqrt{5}$,点A到底面BCD的距离为1,E为棱BC的中点.
如图,在正三棱锥A-BCD中,AB=$\sqrt{5}$,点A到底面BCD的距离为1,E为棱BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 收入x(万元) | 8.0 | 8.6 | 10.0 | 11.4 | 12.0 |
| 支出y(万元) | 4.1 | 5.2 | 6.1 | 6.7 | 7.9 |
| A. | 9.05万元 | B. | 9.25万元 | C. | 9.75万元 | D. | 10.25万元 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| p(k2≥k0) | 0.050 | 0.010 | 0.001 |
| k0 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①④ | B. | ②③ | C. | ①②③ | D. | ①③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com