
| A. | ①④ | B. | ②③ | C. | ①②③ | D. | ①③④ |
分析 根据狄利克雷函数,分别讨论当x∈Q和x∈∁RQ时,对应命题是否成立即可.
解答 解:①当x∈Q,则f(x)=1,f(1)=1,则[f(x)]=1,
当x∈∁RQ,则f(x)=0,f(0)=1,则[f(x)]=1,即对任意x∈R,都有f[f(x)]=1,故①正确,
②当x∈Q,则-x∈Q,则f(-x)=1,f(x)=1,此时f(-x)=f(x),
当x∈∁RQ,则-x∈∁RQ,则f(-x)=0,f(x)=0,此时f(-x)=f(x),
即恒有f(-x)=f(x),即函数f(x)是偶函数,故②错误,
③当x1∈Q,有x2∈Q,则x1+x2∈Q,此时f(x1+x2 )=f(x1)=1;
当x1∈∁RQ,有x2∈Q,则x1+x2∈∁RQ,此时f(x1+x2 )=f(x1)=0;
综上恒有f(x1+x2 )=f(x1)成立,故③正确,
④∵f(x)≥0恒成立,∴对任意a,b∈(-∞,0),都有{x|f(x)>a}={x|f(x)>b}=R,故④正确,
故正确的命题是①③④,
故选:D
点评 本题主要考查命题的真假判断,涉及新定义,正确理解狄利克雷函数的分段函数意义是解决本题的关键.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:高中数学 来源: 题型:填空题
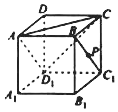 在正方体ABCD-A1B1C1D1中(如图),已知点P在直线BC1上运动.则下列四个命题:
在正方体ABCD-A1B1C1D1中(如图),已知点P在直线BC1上运动.则下列四个命题:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 9 | C. | 10 | D. | 11 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com