
| A. | (-1,1) | B. | $(0,\frac{2}{3})$ | C. | $(\frac{1}{3},1)$ | D. | (0,1) |
分析 解法一,在线段PA的延长线上取点Q,使得PA=AQ,连接OQ,交圆于C,可得∠BOP=∠AOP=∠AOQ=60°,PB=$\sqrt{3}$,故B,O,Q三点共线,且BQ=3,2$\overrightarrow{PA}$=$\overrightarrow{PQ}$,⇒$\overrightarrow{BM}=λ\overrightarrow{BQ}$.由点M在圆O的内部(不包括边界),∴0<$λ<\frac{2}{3}$
解法二:以O为原点,$\overrightarrow{OP}$的方向为x轴正方向建立平面直角坐标系,则P(2,0)
A($\frac{1}{2},\frac{\sqrt{3}}{2}$),B($\frac{1}{2}$,-$\frac{\sqrt{3}}{2}$),设M(x0,y0),得${x}_{0}=\frac{1}{2}(1-3λ)$,y0=$\frac{\sqrt{3}}{2}(3λ-1)$,
得$\frac{1}{4}(1-3λ)^{2}+\frac{3}{4}(3λ-1)^{2}<1$,解得0<$λ<\frac{2}{3}$
解答 解法一:如图,在线段PA的延长线上取点Q,使得PA=AQ,连接OQ,交圆于C,
由圆的半径为1,PO=2可得∠BOP=∠AOP=∠AOQ=60°,PB=$\sqrt{3}$,故B,O,Q三点共线,且BQ=3
因为2$\overrightarrow{PA}$=$\overrightarrow{PQ}$,∴$\overrightarrow{PM}=2λ\overrightarrow{PA}+(1-λ)\overrightarrow{PB}$=λ$\overrightarrow{PQ}$+(1-λ)$\overrightarrow{PB}$.⇒$\overrightarrow{BM}=λ\overrightarrow{BQ}$.
由点M在圆O的内部(不包括边界),∴0<$λ<\frac{2}{3}$
故选:B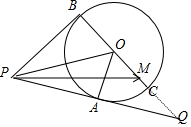
解法二:以O为原点,$\overrightarrow{OP}$的方向为x轴正方向建立平面直角坐标系,则P(2,0)
A($\frac{1}{2},\frac{\sqrt{3}}{2}$),B($\frac{1}{2}$,-$\frac{\sqrt{3}}{2}$),设M(x0,y0),
由$\overrightarrow{PM}=2λ\overrightarrow{PA}+(1-λ)\overrightarrow{PB}$.得${x}_{0}=\frac{1}{2}(1-3λ)$,y0=$\frac{\sqrt{3}}{2}(3λ-1)$,
∵M(x0,y0)在圆O的内部(不包括边界),∴$\frac{1}{4}(1-3λ)^{2}+\frac{3}{4}(3λ-1)^{2}<1$,
整理得-1<3λ-1<1,解得0<$λ<\frac{2}{3}$
故选:B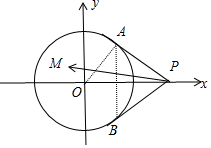
点评 本题考查了平面向量的基本定理,向量的坐标运算,考查了转化思想、数形结合思想,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
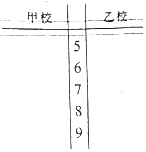 某市对创“市级示范性学校”的甲、乙两所学校进行复查验收,对办学的社会满意度一项评价随机访问了20位市民,这20位市民对这两所学校的评分(评分越高表明市民的评价越好)的数据如下:
某市对创“市级示范性学校”的甲、乙两所学校进行复查验收,对办学的社会满意度一项评价随机访问了20位市民,这20位市民对这两所学校的评分(评分越高表明市民的评价越好)的数据如下:查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
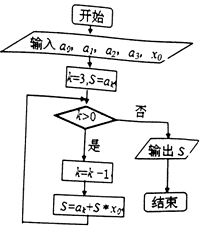 秦九韶是我国南宋时代的数学家,其代表作《数书九章》是我国13世纪数学成就的代表之一;如图是秦九韶算法的一个程序框图,则输出的S为( )
秦九韶是我国南宋时代的数学家,其代表作《数书九章》是我国13世纪数学成就的代表之一;如图是秦九韶算法的一个程序框图,则输出的S为( )| A. | a1+x0(a3+x0(a0+a2x0))的值 | B. | a3+x0(a2+x0(a1+a0x0))的值 | ||
| C. | a0+x0(a1+x0(a2+a3x0))的值 | D. | a2+x0(a0+x0(a3+a1x0))的值 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 第一次 | 第二次 | 第三次 | 第四次 | 第五次 | |
| 参会人数x(万人) | 11 | 9 | 8 | 10 | 12 |
| 原材料t(袋) | 28 | 23 | 20 | 25 | 29 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
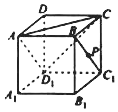 在正方体ABCD-A1B1C1D1中(如图),已知点P在直线BC1上运动.则下列四个命题:
在正方体ABCD-A1B1C1D1中(如图),已知点P在直线BC1上运动.则下列四个命题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com