练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
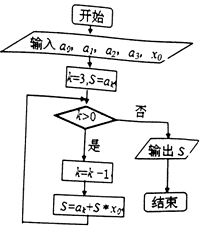
    19．秦九韶是我国南宋时代的数学家，其代表作《数书九章》是我国13世纪数学成就的代表之一；如图是秦九韶算法的一个程序框图，则输出的S为（　　）
    A．a1+x0（a3+x0（a0+a2x0））的值B．a3+x0（a2+x0（a1+a0x0））的值
    C．a0+x0（a1+x0（a2+a3x0））的值D．a2+x0（a0+x0（a3+a1x0））的值

    分析 由已知中的程序语句可知：该程序的功能是利用循环结构计算并输出变量S的值，模拟程序的运行过程，分析循环中各变量值的变化情况，可得答案．

    解答 解：模拟程序的运行，可得
    k=3时，S=a3，
    k=2时，S=a2+a3x0，
    k=1时，S=a1+（a2+a3x0）x0，
    k=0时，S=a0+x0（a1+（a2+a3x0）x0），
    由题意，此时不满足条件，退出循环，输出S的值为a0+x0（a1+（a2+a3x0）x0）的值．
    故选：C．

    点评 本题考查了程序框图的应用问题，解题时应模拟程序框图的运行过程，以便得出正确的结论，是基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    9．在极坐标系中，以极点为坐标原点，极轴为x轴正半轴，建立直角坐标系，点M（2，$\frac{π}{6}}$）的直角坐标是（$\sqrt{3}，1$）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．设全集U={x∈R|x＞0}，函数f（x）=$\frac{1}{\sqrt{lnx-1}}$的定义域为A，则∁UA为（　　）
    A．（0，e]B．（0，e）C．（e，+∞）D．[e，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．襄阳农科所对冬季昼夜温差大小与某反季节大豆新品种发芽多少之间的关系进行分析研究，他们分别记录了12月1日至12月5日的每天昼夜温度与实验室每天每100颗种子中的发芽数，得到如下数据：
    日期12月1日12月2日12月3日12月4日12月5日
    温差x（℃）101113128
    发芽数y（颗）2326322616
    襄阳农科所确定的研究方案是：先从这5组数据中选取2组，用剩下的3组数据求线性回归方程，再对被选取的2组数据进行检验．
    （1）求选取的2组数据恰好是不相邻的2天数据的概率；
    （2）若选取的是12月1日与12月5日这两组数据，情根据12月2日至12月4日的数据，求y关于x的线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$；
    （3）若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过1颗，则认为得到的线性回归方程是可靠的，试问（2）中所得的线性回归方程是否可靠？
    注：$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}•\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n•{\overline{x}}^{2}}$=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）•（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}$，$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$•$\overline{x}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．已知直线PA，PB分别与半径为1的圆O相切于点A，B，PO=2，$\overrightarrow{PM}=2λ\overrightarrow{PA}+（1-λ）\overrightarrow{PB}$．若点M在圆O的内部（不包括边界），则实数λ的取值范围是（　　）
    A．（-1，1）B．$（0，\frac{2}{3}）$C．$（\frac{1}{3}，1）$D．（0，1）

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    4．从3名男同学和2名女同学中任选2名参加体能测试，则恰有1名男同学参加体能测试的概率为$\frac{3}{5}$．（结果用最简分数表示）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．某公司为了准确地把握市场，做好产品生产计划，对过去四年的数据进行整理得到了第x年与年销量y（单位：万件）之间的关系如表：
    x1234
    y12284256
    （Ⅰ）在图中画出表中数据的散点图；
    （Ⅱ）根据（Ⅰ）中的散点图拟合y与x的回归模型，并用相关系数加以说明；
    （Ⅲ）建立y关于x的回归方程，预测第5年的销售量约为多少？．
    附注：参考数据：$\sqrt{\sum_{i=1}^4{{{（{y_i}-\overline y）}^2}}}≈32.6$，$\sqrt{5}≈2.24$，$\sum_{i=1}^4{{x_i}{y_i}=418}$．
    参考公式：相关系数$r=\frac{{\sum_{i=1}^n{（{x_i}-\overline x）（{y_i}-\overline y）}}}{{\sqrt{\sum_{i=1}^n{{{（{x_i}-\overline x）}^2}}\sum_{i=1}^n{{{（{y_i}-\overline y）}^2}}}}}$，
    回归方程$\widehaty=\widehata+\widehatbx$中斜率和截距的最小二乘法估计公式分别为：$\widehatb=\frac{{\sum_{i=1}^n{（{x_i}-\overline x）（{y_i}-\overline y）}}}{{\sum_{i=1}^n{{{（{x_i}-\overline x）}^2}}}}=\frac{{\sum_{i=1}^n{{x_i}{y_i}}-n\overline x\overline y}}{{\sum_{i=1}^n{x_i^2}-n{{\overline x}^2}}}$，$\widehata=\overline y-\widehatb\overline x$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    8．总体由编号为01，02，…，29，30的30个个体组成．利用下面的随机数表选取4个个体．选取方法是从随机数表第1行的第5列和第6列数字开始由左到右依次选取两个数字，则选出的第4个个体的编号为29
    7806　6572　0802　6314　2947　1821　9800
    3204　9234　4935　3623　4869　6938　7481

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    17．在对人们的休闲方式的一次调查中，共调查 了100人，其中女性55人，男性45人．女性中有40人主要的休闲方式是看电视，另外15人主要的休闲方式是运动；男性中有20人主要休闲方式是看电视，另外25人主要休闲方式是运动．
    （1）根据以上数据建立一个2×2的列联表．
    （2）是否有99%的把握认为性别与休闲方式有关系？${K^2}=\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$
    p（k2≥k0）0.0500.0100.001
    k03.8416.63510.828

    查看答案和解析>>

    同步练习册答案