
 ij��˾Ϊ��ȷ�ذ����г������ò�Ʒ�����ƻ����Թ�ȥ��������ݽ��������õ��˵�x����������y����λ�������֮��Ĺ�ϵ�����
ij��˾Ϊ��ȷ�ذ����г������ò�Ʒ�����ƻ����Թ�ȥ��������ݽ��������õ��˵�x����������y����λ�������֮��Ĺ�ϵ�����| x | 1 | 2 | 3 | 4 |
| y | 12 | 28 | 42 | 56 |
���� ������ͼ�л�����������ֱ�ӻ���ɢ��ͼ��
�����ݣ����е�ɢ��ͼ���y��x�Ļع�ģ�ͣ�����y��x�����ϵ������Ϊ0.9996��˵��y��x��������س̶��൱��˵�����������Իع�ģ�����y��x�Ĺ�ϵ��
��������ع�ֱ�߷��̣�Ȼ������5�����������
��� �⣺��������ɢ��ͼ��ͼ��
�����ɣ���ɢ��ͼ��֪��������·ֲ���һ��ֱ�߸������������������ο����ݵã�$\overline x=\frac{5}{2}$��$\overline y=\frac{69}{2}$��$\sum_{i=1}^4{{x_i}{y_i}=418}$��$\sqrt{\sum_{i=1}^4{{{��{y_i}-\overline y��}^2}}}��32.6$��$\sum_{i=1}^4{x_i^2}=30$��$\sum_{i=1}^4{��{x_i}-\overline x����{y_i}-\overline y��=\sum_{i=1}^4{{x_i}{y_i}}-\overline x\sum_{i=1}^4{y_i}=418-\frac{5}{2}��138=73}$��$\sqrt{\sum_{i=1}^4{{{��{x_i}-\overline x��}^2}}}=\sqrt{\sum_{i=1}^4{{x_i}^2-n{{\overline x}^2}}}=\sqrt{30-4��{{��\frac{5}{2}��}^2}}=\sqrt{5}��2.24$��$r=\frac{{\sum_{i=1}^4{��{x_i}-\overline x����{y_i}-\overline y��}}}{{\sqrt{\sum_{i=1}^4{{{��{x_i}-\overline x��}^2}}\sum_{i=1}^4{{{��{y_i}-\overline y��}^2}}}}}=\frac{73}{2.24��32.6}��0.9996$��
��y��x�����ϵ������Ϊ0.9996��˵��y��x��������س̶��൱��
����������Իع�ģ�����y��x�Ĺ�ϵ��
�����ɣ���֪��$\overline x=\frac{5}{2}$��$\overline y=\frac{69}{2}$��$\sum_{i=1}^4{{x_i}{y_i}=418}$��$\sum_{i=1}^4{x^2}=30$��$\sum_{i=1}^4{��{x_i}-\overline x}{��^2}=5$��$\widehatb=\frac{{\sum_{i=1}^n{{x_i}{y_i}}-n\overline x\overline y}}{{\sum_{i=1}^n{x_i^2}-n{{\overline x}^2}}}=\frac{73}{5}$��$\widehata=\overline y-\widehatb\overline x=\frac{69}{2}-\frac{73}{5}��\frac{5}{2}=-2$��
��y����x�Ļع�ֱ�߷���Ϊ$\widehaty=\frac{73}{5}x-2$��
��x=5ʱ��$\widehaty=\frac{73}{5}��5-2=71$��
���Ե�5���������ԼΪ71�����
���� ���⿼��ع�ֱ�߷��̵�Ӧ�ã�ɢ��ͼ�Ļ������������������


 ���100�ֵ�Ԫ�Ż�������ϵ�д�
���100�ֵ�Ԫ�Ż�������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
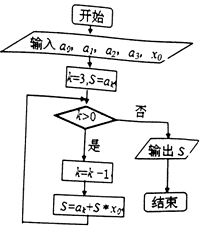 �ؾ������ҹ�����ʱ������ѧ�ң����������������¡����ҹ�13������ѧ�ɾ͵Ĵ���֮һ����ͼ���ؾ����㷨��һ�������ͼ���������SΪ��������
�ؾ������ҹ�����ʱ������ѧ�ң����������������¡����ҹ�13������ѧ�ɾ͵Ĵ���֮һ����ͼ���ؾ����㷨��һ�������ͼ���������SΪ��������| A�� | a1+x0��a3+x0��a0+a2x0������ֵ | B�� | a3+x0��a2+x0��a1+a0x0������ֵ | ||
| C�� | a0+x0��a1+x0��a2+a3x0������ֵ | D�� | a2+x0��a0+x0��a3+a1x0������ֵ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ��һ�� | �ڶ��� | ������ | ���Ĵ� | ����� | |
| �λ�����x�����ˣ� | 11 | 9 | 8 | 10 | 12 |
| ԭ����t������ | 28 | 23 | 20 | 25 | 29 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 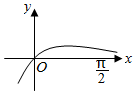 | B�� |  | ||
| C�� | 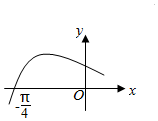 | D�� |  |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��$\frac{3}{4}$��+�ޣ� | B�� | [1��+�ޣ� | C�� | ��$\frac{3}{4}$��1] | D�� | {1} |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com