
| 第一次 | 第二次 | 第三次 | 第四次 | 第五次 | |
| 参会人数x(万人) | 11 | 9 | 8 | 10 | 12 |
| 原材料t(袋) | 28 | 23 | 20 | 25 | 29 |
分析 (Ⅰ)根据表中数据求出$\overline{x}$,$\overline{y}$,即可求出$\stackrel{∧}{b}$,在求出$\stackrel{∧}{a}$,可得线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$
(Ⅱ)由(Ⅰ)的线性回归方程,当x=12时,求出$\stackrel{∧}{y}$,减去12可得补充原材料的袋数.
解答 解:(Ⅰ)根据表中数据可得$\overline{x}$=$\frac{11+9+8+10+12}{5}=10$,$\overline{y}$=$\frac{28+23+20+25+29}{5}=25$.
则:$\sum_{i=1}^{5}({x}_{i}-\overline{x})({y}_{i}-\overline{y})$=(1×3)+(-1)×(-2)+(-2)×(-5)+0+2×4=23.
$\sum_{i=1}^{5}({x}_{i}-\overline{x})^{2}$=1+(-1)2+(-2)2+0+22=10
由公式,得$\stackrel{∧}{b}$=2.3.
线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$,代入可得$\stackrel{∧}{a}$=2.
∴y关于x的线性回归方程为:$\stackrel{∧}{y}$=2.3x+2.
(Ⅱ)由题意,当x=12时,可得出$\stackrel{∧}{y}$=31.9
故而31.9-12=19.9≈20袋.
所以,该店应至少再补充原材料20袋.
点评 本题考查线性回归方程的求法,考查最小二乘法,属于基础题


科目:高中数学 来源: 题型:选择题
| A. | 0.6826 | B. | 0.3413 | C. | 0.4603 | D. | 0.9207 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,1) | B. | $(0,\frac{2}{3})$ | C. | $(\frac{1}{3},1)$ | D. | (0,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
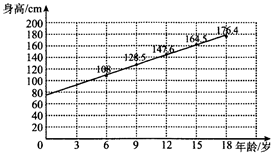 某青少年成长关爱机构为了调研所在地区青少年的年龄与身高壮况,随机抽取6岁,9岁,12岁,15岁,18岁的青少年身高数据各1000个,根据各年龄段平均身高作出如图所示的散点图和回归直线L.根据图中数据,下列对该样本描述错误的是( )
某青少年成长关爱机构为了调研所在地区青少年的年龄与身高壮况,随机抽取6岁,9岁,12岁,15岁,18岁的青少年身高数据各1000个,根据各年龄段平均身高作出如图所示的散点图和回归直线L.根据图中数据,下列对该样本描述错误的是( )| A. | 据样本数据估计,该地区青少年身高与年龄成正相关 | |
| B. | 所抽取数据中,5000名青少年平均身高约为145cm | |
| C. | 直线L的斜率的值近似等于样本中青少年平均身高每年的增量 | |
| D. | 从这5种年龄的青少年中各取一人的身高数据,由这5人的平均年龄和平均身高数据作出的点一定在直线L上 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某公司为了准确地把握市场,做好产品生产计划,对过去四年的数据进行整理得到了第x年与年销量y(单位:万件)之间的关系如表:
某公司为了准确地把握市场,做好产品生产计划,对过去四年的数据进行整理得到了第x年与年销量y(单位:万件)之间的关系如表:| x | 1 | 2 | 3 | 4 |
| y | 12 | 28 | 42 | 56 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com