
分析 (1)利用数列的通项公式化简求解递推关系式即可.
(2)通过当n=1时,当n=2时,当n=3时,计算结果猜想:当n≥3时,an<bn,然后利用数学归纳法的坐标方法证明即可.
解答 解:(1)${a_n}=cos\frac{π}{{3×{2^{n-2}}}}$=$cos\frac{2π}{{3×{2^{n-1}}}}$═$2{({cos\frac{π}{{3×{2^{n-1}}}}})^2}-1$∴${a_n}=2{a_{n+1}}^2-1$
∴${a_{n+1}}=±\sqrt{\frac{{{a_n}+1}}{2}}$
又n∈N*,n+1≥2,an+1>0∴${a_{n+1}}=\sqrt{\frac{{{a_n}+1}}{2}}$…(3分)
(2)当n=1时,${a_1}=-\frac{1}{2}$,b1=1-2=-1,∴a1>b1
当n=2时,${a_2}=\frac{1}{2}$,${b_2}=1-\frac{1}{2}=\frac{1}{2}$,∴a2=b2
当n=3时,${a_3}=\frac{{\sqrt{3}}}{2}$,${b_3}=1-\frac{1}{9}=\frac{8}{9}$,∴a3<b3…(4分)
猜想:当n≥3时,an<bn,…(5分)
下面用数学归纳法证明:
证:①当n=3时,由上知,a3<b3,结论成立.
②假设n=k,k≥3,n∈N*时,ak<bk成立,即${a_k}<1-\frac{2}{k•k!}$
则当n=k+1,${a_{k+1}}=\sqrt{\frac{{{a_k}+1}}{2}}$$<\sqrt{\frac{{2-\frac{2}{k•k!}}}{2}}$=$\sqrt{1-\frac{1}{k•k!}}$,${b_{k+1}}=1-\frac{2}{{({k+1})•({k+1})!}}$
要证ak+1<bk+1,即证明${({\sqrt{1-\frac{1}{k•k!}}})^2}$$<{({1-\frac{2}{{({k+1})•({k+1})!}}})^2}$
即证明$1-\frac{1}{k•k!}$$<1-\frac{4}{{({k+1})•({k+1})!}}+{({\frac{2}{{({k+1})•({k+1})!}}})^2}$
即证明$\frac{1}{k•k!}-\frac{4}{{({k+1})•({k+1})!}}+{({\frac{2}{{({k+1})•({k+1})!}}})^2}>0$
即证明$\frac{{{{({k-1})}^2}}}{{k({k+1})•({k+1})!}}+{({\frac{2}{{({k+1})•({k+1})!}}})^2}>0$,显然成立.
∴n=k+1时,结论也成立.
综合①②可知:当n≥3时,an<bn成立.
综上可得:当n=1时,a1>b1;当n=2时,a2=b2
当n≥3,n∈N*时,an<bn …(10分)
点评 本题考查数列的递推关系式的应用,数学归纳法的应用,考查逻辑推理能力以及计算能力.


科目:高中数学 来源: 题型:解答题
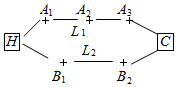 如图,李先生家住H小区,他工作在C处科技园区,从家开车到公司上班路上有L1、L2两条路线,L1路线上有A1、A2、A3三个路口,各路口遇到红灯的概率均为$\frac{1}{2}$;L2路线上有B1、B2两个路口,各路口遇到红灯的概率依次为$\frac{3}{4}$,$\frac{3}{5}$.
如图,李先生家住H小区,他工作在C处科技园区,从家开车到公司上班路上有L1、L2两条路线,L1路线上有A1、A2、A3三个路口,各路口遇到红灯的概率均为$\frac{1}{2}$;L2路线上有B1、B2两个路口,各路口遇到红灯的概率依次为$\frac{3}{4}$,$\frac{3}{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 第一次 | 第二次 | 第三次 | 第四次 | 第五次 | |
| 参会人数x(万人) | 11 | 9 | 8 | 10 | 12 |
| 原材料t(袋) | 28 | 23 | 20 | 25 | 29 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
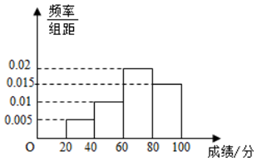 随着社会的发展,食品安全问题渐渐成为社会关注的热点,为了提高学生的食品安全意识,某学校组织全校学生参加食品安全知识竞赛,成绩的频率分布直方图如图所示,数据的分组依次为[20,40),[40,60),[60,80),[80,100),若该校的学生总人数为3000,则成绩不超过60分的学生人数大约为900.
随着社会的发展,食品安全问题渐渐成为社会关注的热点,为了提高学生的食品安全意识,某学校组织全校学生参加食品安全知识竞赛,成绩的频率分布直方图如图所示,数据的分组依次为[20,40),[40,60),[60,80),[80,100),若该校的学生总人数为3000,则成绩不超过60分的学生人数大约为900.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(\begin{array}{l}{0}&{5}\\{3}&{4}\end{array})$ | B. | $(\begin{array}{l}{1}&{0}\\{2}&{3}\end{array})$ | C. | $(\begin{array}{l}{1}&{5}\\{2}&{3}\end{array})$ | D. | $(\begin{array}{l}{1}&{0}\\{2}&{4}\end{array})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 调查某学校学生的课外活动情况,制成等高条形图如图所示,则有较大把握判断:该校学生课外喜欢体育活动还是文娱活动与性别有(填“有”或“无”)关.
调查某学校学生的课外活动情况,制成等高条形图如图所示,则有较大把握判断:该校学生课外喜欢体育活动还是文娱活动与性别有(填“有”或“无”)关.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com