
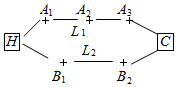 如图,李先生家住H小区,他工作在C处科技园区,从家开车到公司上班路上有L1、L2两条路线,L1路线上有A1、A2、A3三个路口,各路口遇到红灯的概率均为$\frac{1}{2}$;L2路线上有B1、B2两个路口,各路口遇到红灯的概率依次为$\frac{3}{4}$,$\frac{3}{5}$.
如图,李先生家住H小区,他工作在C处科技园区,从家开车到公司上班路上有L1、L2两条路线,L1路线上有A1、A2、A3三个路口,各路口遇到红灯的概率均为$\frac{1}{2}$;L2路线上有B1、B2两个路口,各路口遇到红灯的概率依次为$\frac{3}{4}$,$\frac{3}{5}$.分析 (1)走L2路线,遇到红灯次数X的取值为0,1,2.利用相互独立事件、互斥事件的概率计算公式即可得出概率、分布列及其数学期望.
(2)走L1路线,遇到红灯次数ξ~B$(3,\frac{1}{2})$,可得Eξ.比较Eξ与EX的大小关系即可得出结论.
解答 解:(1)走L2路线,遇到红灯次数X的取值为0,1,2.
P(X=0)=$(1-\frac{3}{4})×(1-\frac{3}{5})$=$\frac{1}{10}$,P(X=1)=$(1-\frac{3}{4})$×$\frac{3}{5}$+$\frac{3}{4}$×$(1-\frac{3}{5})$=$\frac{9}{20}$,P(X=2)=$\frac{3}{4}×\frac{3}{5}$=$\frac{9}{20}$.
∴X分布列为:
| X | 0 | 1 | 2 |
| P | $\frac{1}{10}$ | $\frac{9}{20}$ | $\frac{9}{20}$ |
点评 本题考查了相互独立事件、互斥事件的概率计算公式、二项分布列的计算与数学期望,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{1}{3}$,1) | B. | [$\frac{1}{3}$,$\frac{2}{3}$) | C. | (0,$\frac{2}{3}$) | D. | ($\frac{2}{3}$,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,1) | B. | (-2,-1) | C. | (-2,1) | D. | (1,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0.6826 | B. | 0.3413 | C. | 0.4603 | D. | 0.9207 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com