
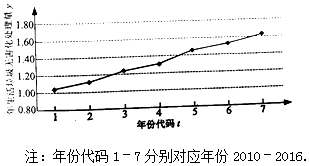
分析 (Ⅰ)由折线图中数据和附注中参考数据,计算相关系数,根据相关系数的值得出结论;
(Ⅱ)计算回归系数,写出y关于t的回归方程;将2018年对应的t值代入回归方程,计算对应的函数值即可.
解答 解:(Ⅰ)由折线图中数据和附注中参考数据得$\overline t=4$,
$\sum_{i=1}^7{{{({t_i}-\overline t)}^2}}=28$,
$\sqrt{\sum_{i=1}^7{{{({y_i}-\overline y)}^2}}}=0.55$,
$\sum_{i=1}^7{({t_i}-\overline t)({y_i}-\overline y)}=\sum_{i=1}^7{{t_i}{y_i}-\overline t\sum_{i=1}^7{y_i}}=40.17-4×9.32=2.89$,
所以相关系数为$r≈\frac{2.89}{0.55×2×2.646}≈0.99$;…(4分)
因为y与t的相关系数近似为0.99,
说明y与t的线性相关程度相当高,从而可以用线性回归模型拟合y与t的关系;…(6分)
(Ⅱ)由$\overline y=\frac{9.32}{7}≈1.331$及(Ⅰ)得,
$\hat b=\frac{{\sum_{i=1}^7{({t_i}-\overline t)({y_i}-\overline y)}}}{{\sum_{i=1}^7{{{({t_i}-\overline t)}^2}}}}=\frac{2.89}{28}≈0.103$,
$\hat a=\overline y-\hat b\overline t≈1.331-0.103×4≈0.92$;
所以,y关于t的回归方程为:$\hat y=0.92+0.10t$;…(10分)
将2018年对应的t=9代入回归方程得:
$\hat y=0.92+0.10×9=1.82$;
所以预测2016年我国生活垃圾无害化处理量将约1.82亿吨…(12分)
点评 本题考查了相关系数与回归直线方程的求法和应用问题,是中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
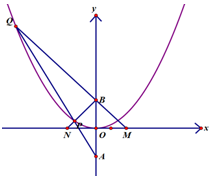 已知抛物线的方程为x2=2py(p>0),过点A(0,-a)(a>0)作直线l与抛物线相交于P,Q两点,点B的坐标为(0,a),连接BP,BQ.且QB,QP与x轴分别交于M,N两点,如果QB的斜率与PB的斜率之积为-3,则∠PBQ=$\frac{2π}{3}$.
已知抛物线的方程为x2=2py(p>0),过点A(0,-a)(a>0)作直线l与抛物线相交于P,Q两点,点B的坐标为(0,a),连接BP,BQ.且QB,QP与x轴分别交于M,N两点,如果QB的斜率与PB的斜率之积为-3,则∠PBQ=$\frac{2π}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{8}$ | B. | $\frac{1}{3}$ | C. | $\frac{3}{8}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\sqrt{4+\frac{π^2}{9}}$ | C. | $\sqrt{1+\frac{π^2}{9}}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 2 | 3 | 4 | 5 | 6 | 7 |
| y | 4.1 | 2.5 | -0.5 | 0.5 | -2.0 | -3.0 |
| A. | $\hat a>0,\hat b>0$ | B. | $\hat a>0,\hat b<0$ | C. | $\hat a<0,\hat b>0$ | D. | $\hat a<0,\hat b<0$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
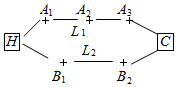 如图,李先生家住H小区,他工作在C处科技园区,从家开车到公司上班路上有L1、L2两条路线,L1路线上有A1、A2、A3三个路口,各路口遇到红灯的概率均为$\frac{1}{2}$;L2路线上有B1、B2两个路口,各路口遇到红灯的概率依次为$\frac{3}{4}$,$\frac{3}{5}$.
如图,李先生家住H小区,他工作在C处科技园区,从家开车到公司上班路上有L1、L2两条路线,L1路线上有A1、A2、A3三个路口,各路口遇到红灯的概率均为$\frac{1}{2}$;L2路线上有B1、B2两个路口,各路口遇到红灯的概率依次为$\frac{3}{4}$,$\frac{3}{5}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com