
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | [$\frac{1}{3}$,1) | B. | [$\frac{1}{3}$,$\frac{2}{3}$) | C. | (0,$\frac{2}{3}$) | D. | ($\frac{2}{3}$,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,1) | B. | (-2,-1) | C. | (-2,1) | D. | (1,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0.6826 | B. | 0.3413 | C. | 0.4603 | D. | 0.9207 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,1) | B. | $(0,\frac{2}{3})$ | C. | $(\frac{1}{3},1)$ | D. | (0,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
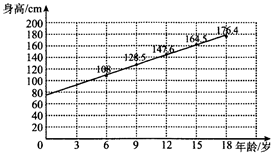 某青少年成长关爱机构为了调研所在地区青少年的年龄与身高壮况,随机抽取6岁,9岁,12岁,15岁,18岁的青少年身高数据各1000个,根据各年龄段平均身高作出如图所示的散点图和回归直线L.根据图中数据,下列对该样本描述错误的是( )
某青少年成长关爱机构为了调研所在地区青少年的年龄与身高壮况,随机抽取6岁,9岁,12岁,15岁,18岁的青少年身高数据各1000个,根据各年龄段平均身高作出如图所示的散点图和回归直线L.根据图中数据,下列对该样本描述错误的是( )| A. | 据样本数据估计,该地区青少年身高与年龄成正相关 | |
| B. | 所抽取数据中,5000名青少年平均身高约为145cm | |
| C. | 直线L的斜率的值近似等于样本中青少年平均身高每年的增量 | |
| D. | 从这5种年龄的青少年中各取一人的身高数据,由这5人的平均年龄和平均身高数据作出的点一定在直线L上 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 收入x(万元) | 8.0 | 8.6 | 10.0 | 11.4 | 12.0 |
| 支出y(万元) | 4.1 | 5.2 | 6.1 | 6.7 | 7.9 |
| A. | 9.05万元 | B. | 9.25万元 | C. | 9.75万元 | D. | 10.25万元 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com