
分析 (1)根据抛物线的定义,丨QF丨=丨QQ1丨,即可求得p的值,即可求得抛物线方程;
(2)设AB的方程,代入椭圆方程,由$\overrightarrow{OA}$•$\overrightarrow{OB}$=0,根据向量数量积的坐标运算及韦达定理,即可求得m的值;
(3)由直线的点斜式方程,求得直线AB的方程,代入椭圆方程,利用韦达定理,即可求得x2=-x1+4k,根据弦长公式,由丨AB丨=丨AD丨,即可求得x1=k-$\frac{1}{k}$,根据三角形的面积公式及基本不等式的性质,即可求得△ABD面积的最小值.
解答 解:(1)设抛物线的C方程x2=2py(p>0),则焦点F(0,$\frac{p}{2}$),准线方程:y=-$\frac{p}{2}$,
过点Q向准线l作垂线,垂足为Q1,
由抛物线的定义可得:丨QF丨=丨QQ1丨,
∴2-(-$\frac{p}{2}$)=3,p=2,
∴抛物线方程:x2=4y;
(2)设直线AB的方程:y=kx+m,则$\left\{\begin{array}{l}{y=kx+m}\\{{x}^{2}=4y}\end{array}\right.$,整理得:x2-4kx-4m=0,
则x1+x2=4k,x1x2=-4m,
由AB为直径的圆经过原点,则$\overrightarrow{OA}$⊥$\overrightarrow{OB}$,$\overrightarrow{OA}$•$\overrightarrow{OB}$=0,
则x1x2+(kx1+m)(kx2+m)=(1+k2)x1x2+km(x1+x2)+m2=0
∴(1+k2)×(-4m)+km×4k+m2=0,整理得m2-4m=0,解得:m=4或m=0,
由m>0,则m=4,
∴m的值4;
(3)设直线AB的斜率为k,k>0,其方程y-y1=k(x-x1),即y=kx+y1-kx1,
∴$\left\{\begin{array}{l}{y=kx+{y}_{1}-k{x}_{1}}\\{{x}^{2}=4y}\end{array}\right.$,整理得:x2-4kx+4kx1-4y1=0,
∴x1+x2=4k,x2=-x1+4k,
丨AB丨2=(1+k2)[(x1+x2)2-4x1x2]=(1+k2)[(x1+x2)2-4x1x2],
=(1+k2)[(4k)2-4x1(-x1+4k)],
=4(1+k2)(x12-4kx1+4k2),
同理丨AD丨=4[1+(-$\frac{1}{k}$)2][x12-4(-$\frac{1}{k}$)x1+4(-$\frac{1}{k}$)2],
=4(1+$\frac{1}{{k}^{2}}$)(x12+$\frac{4}{k}$x1+$\frac{4}{{k}^{2}}$),
由丨AB丨=丨AD丨,则丨AB丨2=丨AD丨2,4(1+k2)(x12-4kx1+4k2),=4(1+$\frac{1}{{k}^{2}}$)(x12+$\frac{4}{k}$x1+$\frac{4}{{k}^{2}}$),
整理得:x1=$\frac{{k}^{2}-1}{k}$=k-$\frac{1}{k}$,
则丨AB丨2=4(1+k2)[(k-$\frac{1}{k}$)2-4k(k-$\frac{1}{k}$)+4k2]=4(1+k2)(k+$\frac{1}{k}$)2,丨AB丨=2$\sqrt{1+{k}^{2}}$(k+$\frac{1}{k}$),
丨AD丨2=4(1+$\frac{1}{{k}^{2}}$)[(k-$\frac{1}{k}$)2+$\frac{4}{k}$(k-$\frac{1}{k}$)+$\frac{4}{{k}^{2}}$]4(1+$\frac{1}{{k}^{2}}$)(k+$\frac{1}{k}$)2,丨AD丨=2$\sqrt{1+\frac{1}{{k}^{2}}}$(k+$\frac{1}{k}$),
∴△ABD面积S=$\frac{1}{2}$×丨AB丨×丨AD丨=$\frac{1}{2}$×2$\sqrt{1+{k}^{2}}$(k+$\frac{1}{k}$)×2$\sqrt{1+\frac{1}{{k}^{2}}}$(k+$\frac{1}{k}$),
=$\frac{2(1+{k}^{2})(k+\frac{1}{k})^{2}}{k}$=2(k+$\frac{1}{k}$)3≥2(2$\sqrt{k×\frac{1}{k}}$)3=16,
当且仅当k=$\frac{1}{k}$时,即k2=1,即k=1,取等号,
∴△ABD面积的最小值16.
点评 本题考查抛物线的性质,直线与抛物线的位置关系,考查韦达定理,弦长公式及基本不等式的应用,考查计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{3}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5π}{6}$ | B. | $\frac{3π}{4}$ | C. | $\frac{2π}{3}$ | D. | $\frac{π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
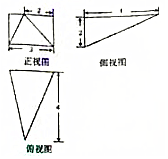
| A. | $3\sqrt{3}$ | B. | $2\sqrt{6}$ | C. | $\sqrt{21}$ | D. | $2\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 停车距离d(米) | (10,20] | (20,30] | (30,40] | (40,50] | (50,60] |
| 频数 | 26 | a | b | 8 | 2 |
| 平均每毫升血液酒精含量x毫克 | 10 | 30 | 50 | 70 | 90 |
| 平均停车距离y米 | 30 | 50 | 60 | 70 | 90 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
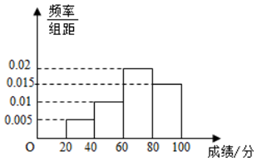 随着社会的发展,食品安全问题渐渐成为社会关注的热点,为了提高学生的食品安全意识,某学校组织全校学生参加食品安全知识竞赛,成绩的频率分布直方图如图所示,数据的分组依次为[20,40),[40,60),[60,80),[80,100),若该校的学生总人数为3000,则成绩不超过60分的学生人数大约为900.
随着社会的发展,食品安全问题渐渐成为社会关注的热点,为了提高学生的食品安全意识,某学校组织全校学生参加食品安全知识竞赛,成绩的频率分布直方图如图所示,数据的分组依次为[20,40),[40,60),[60,80),[80,100),若该校的学生总人数为3000,则成绩不超过60分的学生人数大约为900.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在平面四边形ABCD中,AB=2,AD=$\sqrt{6}$$+\sqrt{2}$,BC=2$\sqrt{3}$,∠ABC=120°,∠DAB=75°
如图,在平面四边形ABCD中,AB=2,AD=$\sqrt{6}$$+\sqrt{2}$,BC=2$\sqrt{3}$,∠ABC=120°,∠DAB=75°查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com