
| 停车距离d(米) | (10,20] | (20,30] | (30,40] | (40,50] | (50,60] |
| 频数 | 26 | a | b | 8 | 2 |
| 平均每毫升血液酒精含量x毫克 | 10 | 30 | 50 | 70 | 90 |
| 平均停车距离y米 | 30 | 50 | 60 | 70 | 90 |
分析 (Ⅰ)根据中位数定义得$\frac{6}{10}a=50-26$,解得a,a+b+36=100,解得b.
(Ⅱ)根据$\hat b=\frac{{\sum_{i=1}^n{{x_i}{y_i}}-n\bar x\bar y}}{{\sum_{i=1}^n{x_i^2}-n{{\bar x}^2}}}$,$\hat a=\bar y-\hat b\bar x$.求出a,b即可.
(Ⅲ)令$\hat y>81$,得0.7x+25>81,解得x>80.
解答 解:(Ⅰ)依题意,得$\frac{6}{10}a=50-26$,解得a=40,(1分)
又a+b+36=100,解得b=24;(2分)
故停车距离的平均数为$15×\frac{26}{100}+25×\frac{40}{100}+35×\frac{24}{100}+45×\frac{8}{100}+55×\frac{2}{100}=27$.(4分)
(Ⅱ)依题意,可知$\overline{x}=50,\overline{y}=60$,(5分)
$\hat b=\frac{10×30+30×50+50×60+70×70+90×90-5×50×60}{{{{10}^2}+{{30}^2}+{{50}^2}+{{70}^2}+{{90}^2}-5×{{50}^2}}}$=$\frac{7}{10}$,
$\hat a=60-\frac{7}{10}×50=25$,
所以回归直线为$\hat y=0.7x+25$.(8分)
(Ⅲ)由(I)知当y>81时认定驾驶员是“醉驾”.(9分)
令$\hat y>81$,得0.7x+25>81,解得x>80,(11分)
当每毫升血液酒精含量大于80毫克时认定为“醉驾”.(12分)
点评 本小题主要考查统计、回归方程等基础知识;考查了数据处理能力、运算求解能力、属于中档题.


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,3) | B. | (0,4) | C. | [3,+∞) | D. | [4,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
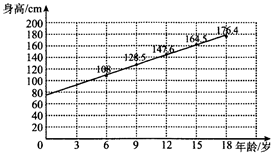 某青少年成长关爱机构为了调研所在地区青少年的年龄与身高壮况,随机抽取6岁,9岁,12岁,15岁,18岁的青少年身高数据各1000个,根据各年龄段平均身高作出如图所示的散点图和回归直线L.根据图中数据,下列对该样本描述错误的是( )
某青少年成长关爱机构为了调研所在地区青少年的年龄与身高壮况,随机抽取6岁,9岁,12岁,15岁,18岁的青少年身高数据各1000个,根据各年龄段平均身高作出如图所示的散点图和回归直线L.根据图中数据,下列对该样本描述错误的是( )| A. | 据样本数据估计,该地区青少年身高与年龄成正相关 | |
| B. | 所抽取数据中,5000名青少年平均身高约为145cm | |
| C. | 直线L的斜率的值近似等于样本中青少年平均身高每年的增量 | |
| D. | 从这5种年龄的青少年中各取一人的身高数据,由这5人的平均年龄和平均身高数据作出的点一定在直线L上 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①②③④ | B. | ②③④ | C. | ①②④ | D. | ①② |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com