
分析 (Ⅰ)根据同角的三角函数的关系以及诱导公式和两角和的正弦公式即可求出,再根据正弦定理即可求出c的值,
(Ⅱ)根据余弦定理和基本不等式即可求出最大值.
解答 解:(Ⅰ)tanA+tanC=$\frac{2sinB}{cosA}$可得$\frac{sinA}{cosA}$+$\frac{sinC}{cosC}$=$\frac{sinAcosC+cosAsinC}{cosAcosC}$
=$\frac{sin(A+C)}{cosAcosC}$=$\frac{sinB}{cosAcosC}$=$\frac{2sinB}{cosA}$,
∴cosC=$\frac{1}{2}$,
∵0<C<π,
∴C=$\frac{π}{3}$,
∵b=$\sqrt{2}$sinB,
由正弦定理可得$\frac{c}{sinC}$=$\frac{b}{sinB}$=$\sqrt{2}$,
∴c=$\frac{\sqrt{6}}{2}$;
(Ⅱ)由余弦定理可得c2=a2+b2-2abcosC,
∴$\frac{3}{2}$=a2+b2-ab≥2ab-ab=ab,当且仅当a=b时取等号.
∴S△ABC=$\frac{1}{2}$absinC=$\frac{\sqrt{3}}{4}$ab≤$\frac{\sqrt{3}}{4}$×$\frac{3}{2}$=$\frac{3\sqrt{3}}{8}$,
故△ABC面积的最大值为$\frac{3\sqrt{3}}{8}$..
点评 本题考查了正弦定理和余弦定理以及三角函数的恒等变换,属于中档题.


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
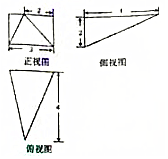
| A. | $3\sqrt{3}$ | B. | $2\sqrt{6}$ | C. | $\sqrt{21}$ | D. | $2\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 停车距离d(米) | (10,20] | (20,30] | (30,40] | (40,50] | (50,60] |
| 频数 | 26 | a | b | 8 | 2 |
| 平均每毫升血液酒精含量x毫克 | 10 | 30 | 50 | 70 | 90 |
| 平均停车距离y米 | 30 | 50 | 60 | 70 | 90 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
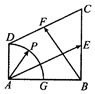 在直角梯形ABCD中,AB⊥AD,AD∥BC,AB=BC=2AD=2,E,F分别为BC,CD的中点,以A为圆心,AD为半径的圆交AB于G,点P在$\widehat{DG}$上运动(如图).若$\overrightarrow{AP}$=λ$\overrightarrow{AE}$+μ$\overrightarrow{BF}$,其中λ,μ∈R,则6λ+μ的取值范围是( )
在直角梯形ABCD中,AB⊥AD,AD∥BC,AB=BC=2AD=2,E,F分别为BC,CD的中点,以A为圆心,AD为半径的圆交AB于G,点P在$\widehat{DG}$上运动(如图).若$\overrightarrow{AP}$=λ$\overrightarrow{AE}$+μ$\overrightarrow{BF}$,其中λ,μ∈R,则6λ+μ的取值范围是( )| A. | [1,$\sqrt{2}$] | B. | [$\sqrt{2}$,2$\sqrt{2}$] | C. | [2,2$\sqrt{2}$] | D. | [1,2$\sqrt{2}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,e) | B. | (1,+∞) | C. | (1,e) | D. | (e,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com