
分析 (1)圆C的普通方程为(x-1)2+y2=1,由x=ρcosθ,y=ρsinθ,能求出圆C的极坐标方程为ρ=2cosθ.
(2)设(ρ1,θ1)为点P的极坐标,由$\left\{\begin{array}{l}{ρ_1}=2cos{θ_1}\\ tan{θ_1}=2\end{array}\right.$,求出$\left\{\begin{array}{l}{ρ_1}=\frac{2}{5}\sqrt{5}\\ tan{θ_1}=2\end{array}\right.$,设(ρ2,θ2)为点Q的极坐标,联立方程组求出$\left\{\begin{array}{l}{ρ_2}=\frac{2}{3}\sqrt{5}\\ tan{θ_2}=2\end{array}\right.$,由θ1=θ2,能求出线段PQ的长.
解答 解:(1)圆C的普通方程为(x-1)2+y2=1,
又x=ρcosθ,y=ρsinθ,
圆C的极坐标方程为ρ=2cosθ.
(2)设(ρ1,θ1)为点P的极坐标,
则有$\left\{\begin{array}{l}{ρ_1}=2cos{θ_1}\\ tan{θ_1}=2\end{array}\right.$,解得$\left\{\begin{array}{l}{ρ_1}=\frac{2}{5}\sqrt{5}\\ tan{θ_1}=2\end{array}\right.$,
设(ρ2,θ2)为点Q的极坐标,
则$\left\{\begin{array}{l}2{ρ_2}(sin{θ_2}cos\frac{π}{4}+cos{θ_2}sin\frac{π}{4})=2\sqrt{2}\\ tan{θ_2}=2\end{array}\right.$,
解得$\left\{\begin{array}{l}{ρ_2}=\frac{2}{3}\sqrt{5}\\ tan{θ_2}=2\end{array}\right.$,
由于θ1=θ2,∴$|PQ|=|{ρ_1}-{ρ_2}|=\frac{4}{15}\sqrt{5}$,
∴线段PQ的长为$\frac{4}{15}\sqrt{5}$.
点评 本题考查圆的极坐标方程的求法,考查线段长的求法,考查极坐标方程、直角坐标方程、参数方程的互化等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | 056,080,104 | B. | 054,078,102 | C. | 054,079,104 | D. | 056,081,106 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
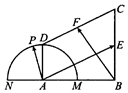 在直角梯形ABCD中,AB⊥AD,AD∥BC,AB=BC=2AD=2,E,F分别为BC,CD的中点,以A为圆心,AD为半径的半圆分别交BA及其延长线于点M,N,点P在$\widehat{MDN}$上运动(如图).若$\overrightarrow{AP}=λ\overrightarrow{AE}+μ\overrightarrow{BF}$,其中λ,μ∈R,则2λ-5μ的取值范围是( )
在直角梯形ABCD中,AB⊥AD,AD∥BC,AB=BC=2AD=2,E,F分别为BC,CD的中点,以A为圆心,AD为半径的半圆分别交BA及其延长线于点M,N,点P在$\widehat{MDN}$上运动(如图).若$\overrightarrow{AP}=λ\overrightarrow{AE}+μ\overrightarrow{BF}$,其中λ,μ∈R,则2λ-5μ的取值范围是( )| A. | [-2,2] | B. | $[{-2,2\sqrt{2}}]$ | C. | $[{-2\sqrt{2},2}]$ | D. | $[{-2\sqrt{2},2\sqrt{2}}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $2\sqrt{5}$ | B. | $4\sqrt{5}$ | C. | 8 | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0.1587 | B. | 0.0228 | C. | 0.0013 | D. | 0.4972 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com