
| A. | $2\sqrt{5}$ | B. | $4\sqrt{5}$ | C. | 8 | D. | 16 |
分析 曲线C转化为y=|x|,直线l转化为:x-2y-2=0,由两点M,N到直线l:ρcosθ-2ρsinθ=2的距离为$\sqrt{5}$,求出m=3,联立$\left\{\begin{array}{l}{x-2y+3=0}\\{y=|x|}\end{array}\right.$,能求出|MN|.
解答 解:∵曲线C:sinθ=|cosθ|,
∴ρsinθ=|ρcosθ|,∴y=|x|,
∵直线l:ρcosθ-2ρsinθ=2,
∴直线l:x-2y-2=0,
d=$\frac{|m+2|}{\sqrt{5}}$=$\sqrt{5}$,∴|m+2|=5,解得m=3或m=-7(舍),
联立$\left\{\begin{array}{l}{x-2y+3=0}\\{y=|x|}\end{array}\right.$,得$\left\{\begin{array}{l}{x=-1}\\{y=1}\end{array}\right.$或$\left\{\begin{array}{l}{x=3}\\{y=3}\end{array}\right.$,
∴M(-1,1),N(3,3),
∴|MN|=$\sqrt{(3-1)^{2}+(3+1)^{2}}$=2$\sqrt{5}$.
故选:A.
点评 本题考查两点间距离的求法,是基础题,解题时要认真审题,注意两点间距离公式的合理运用.


 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
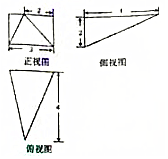
| A. | $3\sqrt{3}$ | B. | $2\sqrt{6}$ | C. | $\sqrt{21}$ | D. | $2\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
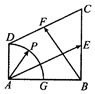 在直角梯形ABCD中,AB⊥AD,AD∥BC,AB=BC=2AD=2,E,F分别为BC,CD的中点,以A为圆心,AD为半径的圆交AB于G,点P在$\widehat{DG}$上运动(如图).若$\overrightarrow{AP}$=λ$\overrightarrow{AE}$+μ$\overrightarrow{BF}$,其中λ,μ∈R,则6λ+μ的取值范围是( )
在直角梯形ABCD中,AB⊥AD,AD∥BC,AB=BC=2AD=2,E,F分别为BC,CD的中点,以A为圆心,AD为半径的圆交AB于G,点P在$\widehat{DG}$上运动(如图).若$\overrightarrow{AP}$=λ$\overrightarrow{AE}$+μ$\overrightarrow{BF}$,其中λ,μ∈R,则6λ+μ的取值范围是( )| A. | [1,$\sqrt{2}$] | B. | [$\sqrt{2}$,2$\sqrt{2}$] | C. | [2,2$\sqrt{2}$] | D. | [1,2$\sqrt{2}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com