
分析 (1)将由$\overrightarrow{OM}$=$\overrightarrow{FN}$,即可求得N点坐标,将M代入抛物线方程,即可求得a,代入椭圆方程,即可求得b的值,即可求得椭圆方程;
(2)①设直线PB的方程,设B,E点坐标,将直线PB代入椭圆方程,求得直线AE的方程,利用韦达定理即可求得x的值,直线AE与x轴相交于定点(1,0);
②设直线l的方程,代入椭圆方程,由△>0,即可求得n的取值范围,利用直线的斜率公式及韦达定理kMA+kMB=0,则直线MA,MB关于直线x=1对称.
解答 解:(1)设N(a,y0),连接MN,由$\overrightarrow{OM}$=$\overrightarrow{FN}$,则OMNF为平行四边形,则y0=$\frac{3}{2}$,
将M(1,$\frac{3}{2}$)代入抛物线方程:解得:a=2,
将M(1,$\frac{3}{2}$)代入椭圆方程:$\frac{1}{4}+\frac{9}{4{b}^{2}}=1$,解得:b2=3,
∴椭圆的标准方程:$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$;
(2)①证明:由题意,直线PB的斜率存在,设直线PB的方程为y=k(x-4),B(x1,y1),E(x2,y2),
则A(x1,-y1),$\left\{\begin{array}{l}{y=k(x-4)}\\{3{x}^{2}+4{y}^{2}=12}\end{array}\right.$,整理得:(3+4k2)x2-32k2x+64k2-12=0,
x1+x2=$\frac{32{k}^{2}}{3+4{k}^{2}}$,x1x2=$\frac{64{k}^{2}-12}{3+4{k}^{2}}$,①
则直线AE的方程为:y-y2=$\frac{{y}_{2}+{y}_{1}}{{x}_{2}-{x}_{1}}$(x-x2),令y=0,x=x2-$\frac{{y}_{2}({x}_{2}-{x}_{1})}{{y}_{1}+{y}_{2}}$,
由y1=k(x1-4),y2=k(x2-4),
∴x=$\frac{2{x}_{1}{x}_{2}-4({x}_{1}+{x}_{2})}{{x}_{1}+{x}_{2}-8}$,
∴x=1,
∴直线AE与x轴相交于定点(1,0);
②由题意可知,直线MF的方程为x=1,则kOM=$\frac{1}{2}$,设直线l:y=$\frac{1}{2}$x+n,(n≠1),
设A(x3,y3),B(x4,y4),$\left\{\begin{array}{l}{y=\frac{1}{2}x+n}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\end{array}\right.$,整理得:x2+nx+n2-3=0,
△=n2-4×(n2-3)=12-3n2>0,即b∈(-2,2),且n≠1,
x3+x4=-n,x3x4=n2-3,
则kMA+kMB=$\frac{{y}_{3}-\frac{3}{2}}{{x}_{3}-1}$+$\frac{{y}_{4}-\frac{3}{2}}{{x}_{4}-1}$=$\frac{\frac{1}{2}{x}_{3}+n-\frac{3}{2}}{{x}_{3}-1}$+$\frac{\frac{1}{2}{x}_{4}+n-\frac{3}{2}}{{x}_{4}-1}$
=1+$\frac{n-1}{{x}_{3}-1}$+$\frac{n-1}{{x}_{4}-1}$=1+$\frac{(n-1)({x}_{1}+{x}_{2}-2)}{{x}_{1}{x}_{2}-({x}_{3}+{x}_{4})+1}$=1-$\frac{(n-1)(n+2)}{{n}^{2}+n-2}$=0,
直线MA,MB关于直线x=1对称.
点评 本题考查椭圆的标准方程,直线与椭圆的位置关系,考查韦达定理,直线的斜率公式,考查计算能力,属于中档题.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
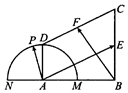 在直角梯形ABCD中,AB⊥AD,AD∥BC,AB=BC=2AD=2,E,F分别为BC,CD的中点,以A为圆心,AD为半径的半圆分别交BA及其延长线于点M,N,点P在$\widehat{MDN}$上运动(如图).若$\overrightarrow{AP}=λ\overrightarrow{AE}+μ\overrightarrow{BF}$,其中λ,μ∈R,则2λ-5μ的取值范围是( )
在直角梯形ABCD中,AB⊥AD,AD∥BC,AB=BC=2AD=2,E,F分别为BC,CD的中点,以A为圆心,AD为半径的半圆分别交BA及其延长线于点M,N,点P在$\widehat{MDN}$上运动(如图).若$\overrightarrow{AP}=λ\overrightarrow{AE}+μ\overrightarrow{BF}$,其中λ,μ∈R,则2λ-5μ的取值范围是( )| A. | [-2,2] | B. | $[{-2,2\sqrt{2}}]$ | C. | $[{-2\sqrt{2},2}]$ | D. | $[{-2\sqrt{2},2\sqrt{2}}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $2\sqrt{5}$ | B. | $4\sqrt{5}$ | C. | 8 | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0.1587 | B. | 0.0228 | C. | 0.0013 | D. | 0.4972 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com