练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    20．已知曲线C1的参数方程为$\left\{\begin{array}{l}{x=1+cosθ}\\{y=sinθ}\end{array}\right.$（θ为参数），曲线C2的极坐标方程为ρ=-2cosθ+4sinθ．
    （Ⅰ）将曲线C1的参数方程化为普通方程，曲线C2的极坐标方程化为直角坐标方程．
    （Ⅱ）曲线C1，C2是否相交，若不相交，请说明理由；若交于一点，则求出此点的极坐标；若交于两点，则求出过两点的直线的极坐标方程．

    分析 （Ⅰ）曲线C1的参数方程消去参数，能求出曲线C1的普通方程，由曲线C2的极坐标方程能求出曲线C2的直角坐标方程．
    （Ⅱ）求出曲线C1、C2的交线为4x-4y=0，即x=y，由此能示出过两点的直线的极坐标方程．

    解答 解：（Ⅰ）∵曲线C1的参数方程为$\left\{\begin{array}{l}{x=1+cosθ}\\{y=sinθ}\end{array}\right.$（θ为参数），
    ∴曲线C1的普通方程为（x-1）2+y2=1，
    ∵曲线C2的极坐标方程为ρ=-2cosθ+4sinθ，
    ∴曲线C2的直角坐标方程为x2+y2+2x-4y=0．
    （Ⅱ）曲线C1是以C1（1，0）为圆心，以r1=1为半径的圆，
    曲线C2是以C2（-1，2）为圆心，以${r}_{2}=\frac{1}{2}\sqrt{4+16}$=$\sqrt{5}$为半径的圆，
    |C1C2|=$\sqrt{4+4}$=2$\sqrt{2}$∈（|r1-r2|，r1+r2），
    ∴曲线C1，C2交于两点，
    ∵曲线C1的普通方程为（x-1）2+y2=1，即x2+y2-2x=0，
    曲线C2的直角坐标方程为x2+y2+2x-4y=0．
    ∴曲线C1、C2的交线为4x-4y=0，即x=y，
    ∴过两点的直线的极坐标方程为tanθ=1，即$θ=\frac{π}{4}$或θ=$\frac{5π}{4}$．

    点评 本题考查曲线的直角坐标方程的求法，考查两圆交线的极坐标方程的求法，考查极坐标方程、直角坐标方程、参数方程的互化，考查推理论证能力、运算求解能力，考查化归与转化思想、函数与方程思想，是中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    10．直角坐标方程的x2+y2-2x+3y=0极坐标方程为ρ=2cosθ-3sinθ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．在一次实验中，测得（x，y）的四组值分别是A（6，2），B（8，3），C（10，5），D（12，6），则y与x之间的回归直线方程为（　　）
    A．$\hat y=2.3x-0.7$B．$\hat y=2.3x+0.7$C．$\hat y=0.7x-2.3$D．$\hat y=0.7x+2.3$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．已知函数f（x）=|$\frac{2}{3}$x+1|．
    （1）若不等式f（x）≥-|x|+a恒成立，求实数a的取值范围；
    （2）若对于实数x，y，有|x+y+1|≤$\frac{1}{3}$，|y-$\frac{1}{3}$|≤$\frac{2}{3}$，求证：f（x）≤$\frac{7}{9}$，
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．曲线y=3lnx+x+2在点p0处的切线与直线x+4y-8=0垂直，则点p0的坐标是（　　）
    A．（0，1）B．（1，0）C．（1，-1）D．（1，3）

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    5．设函数f（x）=$\left\{\begin{array}{l}{{x}^{3}，x≤a}\\{{x}^{2}，x＞a}\end{array}\right.$．若存在实数b，使得函数y=f（x）-bx恰有2个零点，则实数a的取值范围是（-∞，0）∪（0，1）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．某三棱锥的三视图如图所示，已知该三棱锥的外接球的表面积为12π，则此三棱锥的体积为（　　）
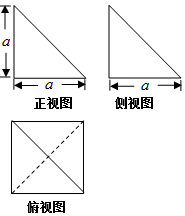
    A．4B．$\frac{4}{3}$C．$\frac{8}{3}$D．$\frac{1}{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．已知右焦点为F的椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）过点M（1，$\frac{3}{2}$），直线x=a与抛物线L：x2=$\frac{8}{3}$y交于点N，且$\overrightarrow{OM}$=$\overrightarrow{FN}$，其中O为坐标原点．
    （1）求椭圆C的方程；
    （2）直线l与椭圆C交于A、B两点．
    ①若直线l与x轴垂直，过点P（4，0）的直线PB交椭圆C于另一点E，证明直线AE与x轴相交于定点；
    ②已知D为椭圆C的左顶点，若l与直线DM平行，判断直线MA，MB是否关于直线FM对称，并说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    10．设圆C满足：①截y轴所得弦长为2；②被x轴分成两段圆弧，其弧长的比为3：1；③圆心到直线l：x-2y=0的距离为d．当d最小时，圆C的面积为2π．

    查看答案和解析>>

    同步练习册答案