
分析 根据题意,由函数的解析式分2种情况讨论:①、若a<2,则有$\left\{\begin{array}{l}{-{2}^{a}=1}\\{a<2}\end{array}\right.$,②、若a≥2,则有$\left\{\begin{array}{l}{lo{g}_{3}({a}^{2}-1)=1}\\{a≥2}\end{array}\right.$,分别求出a的值,综合可得答案.
解答 解:根据题意,函数f(x)=$\left\{\begin{array}{l}-{2^x},x<2\\{log_3}({x^2}-1),x≥2\end{array}$,
若f(a)=1,
分2种情况讨论:
①、若x<2,则有$\left\{\begin{array}{l}{-{2}^{a}=1}\\{a<2}\end{array}\right.$,
此时无解;
②、若a≥2,则有$\left\{\begin{array}{l}{lo{g}_{3}({a}^{2}-1)=1}\\{a≥2}\end{array}\right.$,
解可得a=2,
综合可得a=2;
故答案为:2.
点评 本题考查函数的值,涉及分段函数的求值问题,注意分段求值,需要分段讨论.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | 既有极大值又有极小值 | B. | 有极大值无极小值 | ||
| C. | 既无极大值又无极小值 | D. | 有极小值无极大值 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | (1,0) | C. | (1,-1) | D. | (1,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
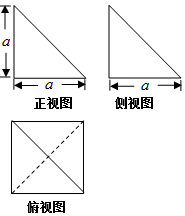
| A. | 4 | B. | $\frac{4}{3}$ | C. | $\frac{8}{3}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 第一次 | 第二次 | 第三次 | 第四次 | 第五次 | |
| 参会人数x(万人) | 11 | 9 | 8 | 10 | 12 |
| 原材料t(袋) | 28 | 23 | 20 | 25 | 29 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com