
分析 (1)利用f'(x)=0得$x=1+\frac{1}{a}$,判断函数的单调性,通过(i)当a≥1时,(ii)当$0<a≤\frac{1}{2}$时,(iii)当$\frac{1}{2}<a<1$时,分别求解函数的最值.
(2)h(x)=af(x+2)+g(x)=aln(x+1)+ex-2x,则$h'(x)=\frac{a}{x+1}+{e^x}-2$,通过①当a≤0时,②当a>0时,i当a≥1时,ii当0<a<1时,利用函数的导数结合函数的单调性求解函数的最值,推出实数a的取值范围.
解答 解:(1)$f'(x)=\frac{1}{x-1}-a=\frac{1+a-ax}{x-1},(x>1)$,由f'(x)=0得$x=1+\frac{1}{a}$,
当$x∈(1,1+\frac{1}{a})$时,f'(x)>0,f(x)为增函数;
当$x∈(1+\frac{1}{a},+∞)$时,f'(x)<0,f(x)为减函数…..(2分)
(i)当a≥1时,$1+\frac{1}{a}≤2$,f(x)在区间[2,3]上为减函数,f(x)min=f(3)=ln2-a
(ii)当$0<a≤\frac{1}{2}$时,$1+\frac{1}{a}≥3$,f(x)在区间[2,3]上为增函数,f(x)min=f(2)=0
(iii)当$\frac{1}{2}<a<1$时,$2<1+\frac{1}{a}<3$,
若$\frac{1}{2}<a<ln2$时,f(x)min=f(2)=0;若ln2≤a<1时,f(x)min=f(3)=ln2-a
综上,当a≥ln2时,f(x)min=ln2-a;当0<a<ln2时,f(x)min=0;…(5分)
(2)h(x)=af(x+2)+g(x)=aln(x+1)+ex-2x,则$h'(x)=\frac{a}{x+1}+{e^x}-2$
①当a≤0时,h'(x)在[0,+∞)上单调递增,则h'(x)≥h'(0)=a-1,∵a-1<0∴存在x0∈(0,+∞),使得h'(x0)=0,于是h(x)在区间(0,x0)上单调递减,当x∈(0,x0)时,h(x)<h(0)=-1与h(x)≥-1恒成立相矛盾,不符合题意….(7分)
②当a>0时,令φ(x)=ex-(x+1),(x≥0)则φ'(x)=ex-1≥0,即φ(x)在[0,+∞)上单调递增,∴φ(x)≥φ(0)=e0-1=0,即ex≥x+1.∴$h'(x)≥\frac{a}{x+1}+({x+1})-2≥2\sqrt{a}-2$
i当a≥1时,h'(x)≥0,于是,h(x)在[0,+∞)上单调递增,∴h(x)≥h(0)=-1恒成立,符合题意
ii当0<a<1时,$h''(x)=-\frac{a}{{{{(x+1)}^2}}}+{e^x}$在[0,+∞)上单调递增,
则h''(x)≥h''(0)=1-a>0,即h'(x)在[0,+∞)上单调递增,所以h'(x)≥h'(0)=a-1∵a-1<0∴存在x0∈(0,+∞),使得h'(x0)=0,于是h(x)在区间(0,x0)上单调递减,
当x∈(0,x0)时,h(x)<h(0)=-1,与h(x)≥-1恒成立相矛盾,不符合题意.
综上,实数a的取值范围是[1,+∞)…..…(12分)
点评 本题考查函数的导数的综合应用,函数的单调性以及函数的最值的求法,二次求导以及函数的最值的转化,考查分析问题解决问题的能力.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
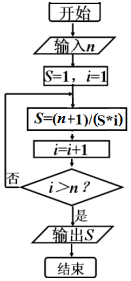
| A. | $\frac{1}{20}$ | B. | $\frac{5}{16}$ | C. | $\frac{16}{5}$ | D. | $\frac{3}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,1) | B. | (-2,-1) | C. | (-2,1) | D. | (1,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,3) | B. | (0,4) | C. | [3,+∞) | D. | [4,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com