
| 日期 | 12月1日 | 12月2日 | 12月3日 | 12月4日 | 12月5日 |
| 温差x(℃) | 10 | 11 | 13 | 12 | 8 |
| 发芽数y(颗) | 23 | 26 | 32 | 26 | 16 |
分析 (1)根据题意列举出从5组数据中选取2组数据共有10种情况,每种情况都是可能出现的,满足条件的事件包括的基本事件有6种.根据等可能事件的概率做出结果.
(2)根据所给的数据,先做出x,y的平均数,即做出本组数据的样本中心点,根据最小二乘法求出线性回归方程的系数,写出线性回归方程.
(3)根据估计数据与所选出的检验数据的误差均不超过1颗,就认为得到的线性回归方程是可靠的,根据求得的结果和所给的数据进行比较,得到所求的方程是可靠的.
解答 解:(1)恰好是不相邻的2天数据的概率P=$1-\frac{4}{C_5^2}=\frac{3}{5}$.
(2)由数据得:$\sum_{i=1}^3{{x_i}{y_i}=11×26+13×32+12×26=1014}$;$\overline x=\frac{1}{3}(11+13+12)=12$,$\overline y=\frac{1}{3}(26+32+26)=28$,$3\overline x•\overline y=3×12×28=1008$;
∴$\sum_{i=1}^n{{x_i}{y_i}-n\overline x•\overline y=}$$\sum_{i=1}^3{{x_i}{y_i}-3\overline x•\overline y=1014-1008=28}$,$\sum_{i=1}^3{x_i^2={{11}^2}+{{13}^2}+{{12}^2}=434}$,$3{\overline x^2}=3×{12^2}=432$;∴$\sum_{i=1}^n{x_i^2-n•{{\overline x}^2}=\sum_{i=1}^3{x_i^2-3•{{\overline x}^2}=}}$434-432=2,
∴$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}•\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n•{\overline{x}}^{2}}$=$\frac{{\sum_{i=1}^3{{x_i}{y_i}-3•\overline x•\overline y}}}{{\sum_{i=1}^3{x_i^2-3•{{\overline x}^2}}}}=\frac{6}{2}=3$;$\hat a=\overline y-\hat b\overline x=28-3×12=-8$.
故y关于x的线性回归方程y=3x-8.
(3)当x=10时,$\hat y=3x-8=3×10-8=22$,|22-23|≤1;
当x=8时,$\hat y=3x-8=3×8-8=16$,|16-16|≤1,故得到的线性回归方程是可靠的.
点评 本题考查线性回归方程的应用,在解题过程中注意对于预报值的估计,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | a>1 | B. | a≤-$\frac{3}{4}$ | C. | a≥1或a<-$\frac{3}{4}$ | D. | a>1或a≤-$\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
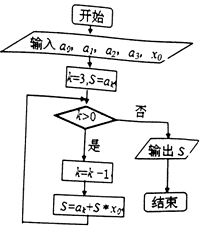 秦九韶是我国南宋时代的数学家,其代表作《数书九章》是我国13世纪数学成就的代表之一;如图是秦九韶算法的一个程序框图,则输出的S为( )
秦九韶是我国南宋时代的数学家,其代表作《数书九章》是我国13世纪数学成就的代表之一;如图是秦九韶算法的一个程序框图,则输出的S为( )| A. | a1+x0(a3+x0(a0+a2x0))的值 | B. | a3+x0(a2+x0(a1+a0x0))的值 | ||
| C. | a0+x0(a1+x0(a2+a3x0))的值 | D. | a2+x0(a0+x0(a3+a1x0))的值 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
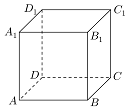 如图,ABCD-A1B1C1D1是棱长为1的正方体,任作平面α与对角线AC1垂直,使得α与正方体的每个面都有公共点,这样得到的截面多边形的面积为S,周长为l的范围分别是[$\frac{\sqrt{3}}{2}$,$\frac{3\sqrt{3}}{4}$]、{3$\sqrt{2}$}(用集合表示)
如图,ABCD-A1B1C1D1是棱长为1的正方体,任作平面α与对角线AC1垂直,使得α与正方体的每个面都有公共点,这样得到的截面多边形的面积为S,周长为l的范围分别是[$\frac{\sqrt{3}}{2}$,$\frac{3\sqrt{3}}{4}$]、{3$\sqrt{2}$}(用集合表示)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com