
分析 (1)数列{an}满足2an-an-1=0,a2=$\frac{2}{3}$.可得an≠0,$\frac{{a}_{n+1}}{{a}_{n}}$=2,利用等比数列的通项公式即可得出an.
(2)数列{(2n-1)an+1}是等差数列,设公差为d,由a4=$\frac{4}{7}$,a2=$\frac{2}{3}$.利用等差数列的通项公式可得d.进而可得an.再利用等差数列的求和公式即可得出.
解答 解:(1)∵数列{an}满足2an-an-1=0,a2=$\frac{2}{3}$.
∴an≠0,$\frac{{a}_{n+1}}{{a}_{n}}$=2,∴a1=$\frac{1}{3}$.
∴数列{an}是等比数列,公比为2,首项为$\frac{1}{3}$.
∴an=$\frac{1}{3}×{2}^{n-1}$.
(2)数列{(2n-1)an+1}是等差数列,设公差为d,∵a4=$\frac{4}{7}$,a2=$\frac{2}{3}$.
∴$7×\frac{4}{7}$+1=$3×\frac{2}{3}$+1+2d,解得d=1.
∴(2n-1)an+1=3×$\frac{2}{3}$+1+(n-2)×1,解得an=$\frac{n}{2n-1}$.
∴$\frac{n}{{a}_{n}}$=2n-1.
∴数列{$\frac{n}{{a}_{n}}$}的前n项和Tn=1+3+…+(2n-1)
=$\frac{n(1+2n-1)}{2}$=n2.
点评 本题考查了等差数列与等比数列的通项公式与求和公式、数列递推关系,考查了推理能力与计算能力,属于中档题.


 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,e] | B. | (0,e) | C. | (e,+∞) | D. | [e,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
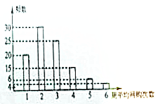 网购是当前民众购物的新方式,某公司为改进营销方式,随机调查了100名市民,统计其周平均网购的次数,并整理得到如下的频数分布直方图.这100名市民中,年龄不超过40岁的有65人将所抽样本中周平均网购次数不小于4次的市民称为网购迷,且已知其中有5名市民的年龄超过40岁.
网购是当前民众购物的新方式,某公司为改进营销方式,随机调查了100名市民,统计其周平均网购的次数,并整理得到如下的频数分布直方图.这100名市民中,年龄不超过40岁的有65人将所抽样本中周平均网购次数不小于4次的市民称为网购迷,且已知其中有5名市民的年龄超过40岁.| 网购迷 | 非网购迷 | 合计 | |
| 年龄不超过40岁 | |||
| 年龄超过40岁 | |||
| 合计 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.01 |
| k0 | 2.072 | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 日期 | 12月1日 | 12月2日 | 12月3日 | 12月4日 | 12月5日 |
| 温差x(℃) | 10 | 11 | 13 | 12 | 8 |
| 发芽数y(颗) | 23 | 26 | 32 | 26 | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0.48 | B. | 0.40 | C. | 0.64 | D. | 0.75 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com