
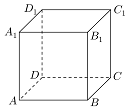
 如图,ABCD-A1B1C1D1是棱长为1的正方体,任作平面α与对角线AC1垂直,使得α与正方体的每个面都有公共点,这样得到的截面多边形的面积为S,周长为l的范围分别是[$\frac{\sqrt{3}}{2}$,$\frac{3\sqrt{3}}{4}$]、{3$\sqrt{2}$}(用集合表示)
如图,ABCD-A1B1C1D1是棱长为1的正方体,任作平面α与对角线AC1垂直,使得α与正方体的每个面都有公共点,这样得到的截面多边形的面积为S,周长为l的范围分别是[$\frac{\sqrt{3}}{2}$,$\frac{3\sqrt{3}}{4}$]、{3$\sqrt{2}$}(用集合表示) 分析 由线面垂直的性质可知截面多边形的边与所在正方形的对角线平行,利用相似比即可得出截面周长为定值,再根据对称性和基本不等式得出面积的最值.
解答 解:连结A1B,A1D,BD,则AC1⊥平面A1BD,
∴AC1⊥A1B
设平面α与平面ABB1A1的交线为EF,
则AC1⊥EF,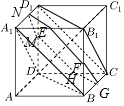
∴EF∥A1B,
同理可得平面α与其他各面的交线都与此平面的对角线平行,
设$\frac{EF}{{A}_{1}B}$=λ,则$\frac{{B}_{1}E}{{A}_{1}{B}_{1}}$=B1E=λ,∴$\frac{DE}{{B}_{1}{D}_{1}}$=1-λ,
∴EF+DE=$\sqrt{2}$λ+$\sqrt{2}$(1-λ)=$\sqrt{2}$,
同理可得六边形其他相邻两边的和为$\sqrt{2}$,
∴六边形的周长l为定值3$\sqrt{2}$.
∴当六边形的边长相等即截面为正六边形时,截面面积最大,
最大面积为$\frac{\sqrt{3}}{4}×(\frac{\sqrt{2}}{2})^{2}×6$=$\frac{3\sqrt{3}}{4}$,
当截面为正三角形时,截面面积最小,
最小面积为$\frac{\sqrt{3}}{4}×(\sqrt{2})^{2}$=$\frac{\sqrt{3}}{2}$.
故答案为:$[\frac{{\sqrt{3}}}{2},\frac{{3\sqrt{3}}}{4}]$,$\{3\sqrt{2}\}$.
点评 本题考查了利用平面几何的知识解决立体几何,考查学生的空间想象能力,属于难题.


科目:高中数学 来源: 题型:解答题
| 日期 | 12月1日 | 12月2日 | 12月3日 | 12月4日 | 12月5日 |
| 温差x(℃) | 10 | 11 | 13 | 12 | 8 |
| 发芽数y(颗) | 23 | 26 | 32 | 26 | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 7806 6572 0802 6314 2947 1821 9800 3204 9234 4935 3623 4869 6938 7481 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0.48 | B. | 0.40 | C. | 0.64 | D. | 0.75 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在正三棱锥A-BCD中,AB=$\sqrt{5}$,点A到底面BCD的距离为1,E为棱BC的中点.
如图,在正三棱锥A-BCD中,AB=$\sqrt{5}$,点A到底面BCD的距离为1,E为棱BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
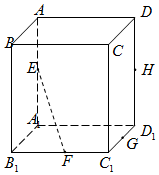 如图,在正方体ABCD-A1B1C1D1中,E,F,G,H分别为棱AA1,B1C1,C1D1,DD1的中点,则下列直线中与直线EF相交的是( )
如图,在正方体ABCD-A1B1C1D1中,E,F,G,H分别为棱AA1,B1C1,C1D1,DD1的中点,则下列直线中与直线EF相交的是( )| A. | 直线CC1 | B. | 直线C1D1 | C. | 直线HC1 | D. | 直线GH |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| p(k2≥k0) | 0.050 | 0.010 | 0.001 |
| k0 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8π | B. | 24π | C. | 48π | D. | 64π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com