
分析 点M的极坐标为(2,$\frac{π}{6}}$),利用极坐标与直角坐标的换算公式能求出点M(2,$\frac{π}{6}}$)的直角坐标.
解答 解:∵点M的极坐标为(2,$\frac{π}{6}}$),
∴x=2×$cos\frac{π}{6}$=$\sqrt{3}$,y=2sin$\frac{π}{6}$=1,
∴点M(2,$\frac{π}{6}}$)的直角坐标是M($\sqrt{3},1$).
故答案为:($\sqrt{3},1$).
点评 本题考查点的直角坐标方程的求法,考查极坐标、直角坐标的互化等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想,是基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
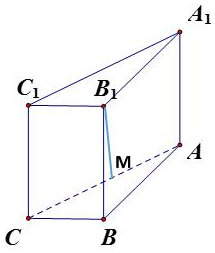 如图,直三棱柱ABC-A1B1C1中,∠ABC=90°,BB1=5,AB=4,BC=2.
如图,直三棱柱ABC-A1B1C1中,∠ABC=90°,BB1=5,AB=4,BC=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-3$\sqrt{3}$,-3) | B. | (3$\sqrt{3}$,-3) | C. | (-3$\sqrt{3}$,3) | D. | (3$\sqrt{3}$,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>1 | B. | a≤-$\frac{3}{4}$ | C. | a≥1或a<-$\frac{3}{4}$ | D. | a>1或a≤-$\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 某市国庆节7天假期的楼房认购量(单位:套)与成交量(单位:套)的折线图如图所示,小明同学根据折线图对这7天的认购量与成交量作出如下判断:①日成交量的中位数是16;②日成交量超过日平均成交量的有2天;③认购量与日期正相关;④10月7日认购量的增幅大于10月7日成交量的增幅.上述判断中错误的个数为( )
某市国庆节7天假期的楼房认购量(单位:套)与成交量(单位:套)的折线图如图所示,小明同学根据折线图对这7天的认购量与成交量作出如下判断:①日成交量的中位数是16;②日成交量超过日平均成交量的有2天;③认购量与日期正相关;④10月7日认购量的增幅大于10月7日成交量的增幅.上述判断中错误的个数为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
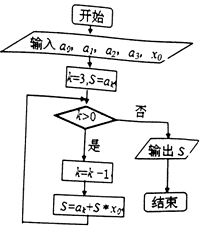 秦九韶是我国南宋时代的数学家,其代表作《数书九章》是我国13世纪数学成就的代表之一;如图是秦九韶算法的一个程序框图,则输出的S为( )
秦九韶是我国南宋时代的数学家,其代表作《数书九章》是我国13世纪数学成就的代表之一;如图是秦九韶算法的一个程序框图,则输出的S为( )| A. | a1+x0(a3+x0(a0+a2x0))的值 | B. | a3+x0(a2+x0(a1+a0x0))的值 | ||
| C. | a0+x0(a1+x0(a2+a3x0))的值 | D. | a2+x0(a0+x0(a3+a1x0))的值 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com