
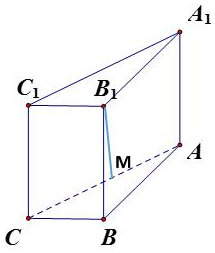
 如图,直三棱柱ABC-A1B1C1中,∠ABC=90°,BB1=5,AB=4,BC=2.
如图,直三棱柱ABC-A1B1C1中,∠ABC=90°,BB1=5,AB=4,BC=2.分析 (1)利用三棱柱${V}_{ABC-{A}_{1}{B}_{1}{C}_{1}}$的体积计算公式即可得出.
(2)连接BM,由直三棱柱ABC-A1B1C1中,可得B1B⊥底面ABC.可得∠B1MB为B1M与平面ABC所成的线面角.在Rt△ABC中,由M是棱AC中点,可得$BM=\frac{1}{2}$AC.在Rt△B1MB中,tan∠B1MB$\frac{{B}_{1}B}{BM}$,即可得出.
解答 解:(1)三棱柱${V}_{ABC-{A}_{1}{B}_{1}{C}_{1}}$的体积V=$\frac{1}{2}×4×2×5$=20.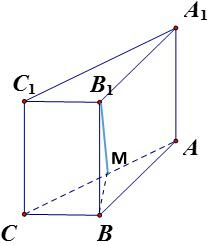
(2)连接BM,由直三棱柱ABC-A1B1C1中,可得B1B⊥底面ABC.
∴∠B1MB为B1M与平面ABC所成的线面角.
在Rt△ABC中,AC$\sqrt{A{B}^{2}+B{C}^{2}}$=$2\sqrt{5}$.
∵M是棱AC中点,$BM=\frac{1}{2}$AC=$\sqrt{5}$.
在Rt△B1MB中,tan∠B1MB$\frac{{B}_{1}B}{BM}$=$\frac{5}{\sqrt{5}}$=$\sqrt{5}$.
∴B1M与平面ABC所成角的大小为arctan$\sqrt{5}$.
点评 本题考查了直三棱柱的性质与体积计算公式、线面角、直角三角形的性质,考查了推理能力与计算能力,属于中档题.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | (2,3) | B. | (-∞,2]∪[3,+∞) | C. | (0,2]∪[3,+∞) | D. | [3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2π}{3}$ | B. | $\frac{4π}{3}$ | C. | 2π | D. | $\frac{8π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?a>2,x1-x2=0 | B. | ?a>2,x1-x2=1 | C. | ?a>2,|x1-x2|=2 | D. | ?a>2,|x1-x2|=3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 年份 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 |
| 年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | a | 5.2 | 5.9 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2x+y-3=0 | B. | x+y-1=0 | C. | x+y-3=0 | D. | 2x-y-5=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com