
| A. | ?a>2,x1-x2=0 | B. | ?a>2,x1-x2=1 | C. | ?a>2,|x1-x2|=2 | D. | ?a>2,|x1-x2|=3 |
分析 通过当x>0时,不妨设其根为x1;当x≤0时,不妨设其根为x2,推出x1-x2=3;转化求出结果即可.
解答 解:当x>0时,y=loga(x+1)+x-2,令y=0,则有loga(x+1)=3-(x+1)不妨设其根为x1;
当x≤0时,$y=x+4-{(\frac{1}{a})^{x+1}}$,令y=0,则有${(\frac{1}{a})^{x+1}}=3+(x+1)$,即:a-(x+1)=3-[-(x+1)],
不妨设其根为x2,则有:(x1+1)+[-(x2+1)]=3,即:x1-x2=3;
同理,若x>0时的零点为x2,x≤0时的零点为x1,则有:x2-x1=3,因而答案为D.
故选:D.
点评 本题考查函数的零点的应用,考查函数与方程的思想,是中档题.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,1) | B. | (-1,0) | C. | (0,1) | D. | (-∞,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
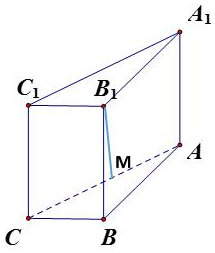 如图,直三棱柱ABC-A1B1C1中,∠ABC=90°,BB1=5,AB=4,BC=2.
如图,直三棱柱ABC-A1B1C1中,∠ABC=90°,BB1=5,AB=4,BC=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 互斥但不相互独立 | B. | 相互独立但不互斥 | ||
| C. | 互斥且相互独立 | D. | 既不相互独立也不互斥 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>1 | B. | a≤-$\frac{3}{4}$ | C. | a≥1或a<-$\frac{3}{4}$ | D. | a>1或a≤-$\frac{3}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com