
分析 根据题意,求出,⊙O:x2+y2=1与x轴的两个交点,可以设出F1、F2的坐标,同时设椭圆的方程为:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1,再依据题意设点P与F1关于直线l:y=$\frac{\sqrt{3}}{3}$(x+4)对称,且P的坐标为(m,n),分析可得$\left\{\begin{array}{l}{\frac{n}{m+1}=-\sqrt{3}}\\{\frac{n}{2}=\frac{\sqrt{3}}{3}(\frac{m-1}{2}+4)}\end{array}\right.$,解可得m、n的值,即可得P的坐标,结合光学知识由椭圆的定义结合光学知识分析可得2a=|EF1|+|EF2|=|EP|+|EF2|=|PF2|,有P、F2的坐标计算可得a的值,由椭圆的几何性质可得b的值,将a、b的值代入椭圆的方程即可得答案.
解答 解:根据题意,⊙O:x2+y2=1与x轴的两个交点为(-1,0),(1,0),
设F1(-1,0),F2(1,0),
要求椭圆的焦点为F1、F2,设其方程为:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1,
设点P与F1关于直线l:y=$\frac{\sqrt{3}}{3}$(x+4)对称,且P的坐标为(m,n),
则有$\left\{\begin{array}{l}{\frac{n}{m+1}=-\sqrt{3}}\\{\frac{n}{2}=\frac{\sqrt{3}}{3}(\frac{m-1}{2}+4)}\end{array}\right.$,
解可得:$\left\{\begin{array}{l}{m=-\frac{5}{2}}\\{n=\frac{3\sqrt{3}}{2}}\end{array}\right.$,
即P的坐标为(-$\frac{5}{2}$,$\frac{3\sqrt{3}}{2}$);
椭圆经过点E,则有2a=|EF1|+|EF2|,
又由点P与F1关于直线l对称,且经过F1的光线与l的交点为E,则|EP|=|EF1|,
则2a=|EF1|+|EF2|=|EP|+|EF2|=|PF2|=$\sqrt{(1+\frac{5}{2})^{2}+(\frac{3\sqrt{3}}{2})^{2}}$=$\sqrt{19}$,
则a=$\frac{\sqrt{19}}{2}$,
又椭圆的半焦距c=1,则b2=a2-c2=$\frac{19}{4}$-1=$\frac{15}{4}$;
则椭圆的方程为:$\frac{{x}^{2}}{\frac{19}{4}}$+$\frac{{y}^{2}}{\frac{15}{4}}$=1;
故答案为:$\frac{{x}^{2}}{\frac{19}{4}}$+$\frac{{y}^{2}}{\frac{15}{4}}$=1.
点评 本题考查椭圆的定义、标准方程,涉及直线间的位置关系,注意利用点关于直线对称的性质进行分析.


科目:高中数学 来源: 题型:选择题
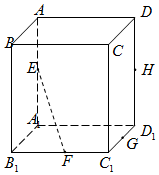 如图,在正方体ABCD-A1B1C1D1中,E,F,G,H分别为棱AA1,B1C1,C1D1,DD1的中点,则下列直线中与直线EF相交的是( )
如图,在正方体ABCD-A1B1C1D1中,E,F,G,H分别为棱AA1,B1C1,C1D1,DD1的中点,则下列直线中与直线EF相交的是( )| A. | 直线CC1 | B. | 直线C1D1 | C. | 直线HC1 | D. | 直线GH |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com