
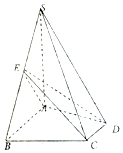
 如图,已知四棱锥S-ABCD中,SA⊥平面ABCD,∠ABC=∠BCD=90°,且SA=AB=BC=2CD,E是边SB的中点.
如图,已知四棱锥S-ABCD中,SA⊥平面ABCD,∠ABC=∠BCD=90°,且SA=AB=BC=2CD,E是边SB的中点.分析 (1)取SA中点F,连接EF,FD,可得EF∥AB,且$EF=\frac{1}{2}AB$,结合∠ABC=∠BCD=90°,得AB∥CD,进一步得到$CD=\frac{1}{2}AB$,从而可得四边形EFDC为平行四边形,得到FD∥EC,再由线面平行的判定可得CE∥面SAD;
(2)在Rt△MCD中,由MC=CD,得∠DMC=45°.在Rt△ABC中,由AB=AC,得∠BCA=45°,可得MD⊥AC,再由线面垂直的性质可得MD⊥SA,进一步由线面垂直的判定可得平面SAC⊥面SMD;
(3)连接AC,BD.由已知可得S△ABC=2S△BCD,得VE-ABC=2VE-BCD,利用等积法得VE-ABCD=3VS-ECD.可得三棱锥S-ECD与四棱锥E-ABCD的体积比为1:3.
解答 (1)证明:取SA中点F,连接EF,FD,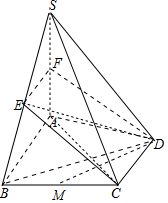
∵E是边SB的中点,∴EF∥AB,且$EF=\frac{1}{2}AB$,
又∵∠ABC=∠BCD=90°,∴AB∥CD,
又∵AB=2CD,即$CD=\frac{1}{2}AB$,
∴EF∥CD,且EF=CD,
∴四边形EFDC为平行四边形,
∴FD∥EC,
又FD?面SAD,CE?面SAD,
∴CE∥面SAD;
(2)证明:在Rt△MCD中,MC=CD,则∠DMC=45°.
在Rt△ABC中,AB=AC,则∠BCA=45°,
∴MD⊥AC,
又SA⊥平面ABCD,且MD?平面ABCD,
∴MD⊥SA,
∴MD⊥面SAC,
∴平面SAC⊥面SMD;
(3)解:连接AC,BD.
∵AB∥CD,且AB=2CD,
∴S△ABC=2S△BCD,
∴VE-ABC=2VE-BCD,
又由S△ACD=S△BCD,得VE-ACD=VE-BCD,
∴VE-ABCD=VE-ACD+VE-ABC=VE-BCD+VE-ABC=3VE-BCD,
∵E是边SB中点,∴S△SCE=S△BCE,
∴VD-SCE=VD-BCE,
又VS-ECD=VD-SCE,VE-BCD=VD-BCE,
∴VE-ABCD=3VS-ECD.
即三棱锥S-ECD与四棱锥E-ABCD的体积比为1:3.
点评 本题考查直线与平面平行、平面与平面垂直的判定,训练了利用等积法求多面体的体积,考查空间想象能力和思维能力,是中档题.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:选择题
| A. | -5 | B. | -4 | C. | $\frac{2}{3}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 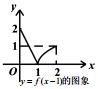 | B. | 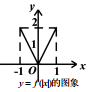 | C. | 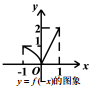 | D. | 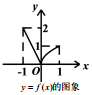 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 6 | C. | 8 | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
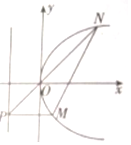 椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的左、右焦点分别为F1,F2,离心率e=$\frac{1}{2}$,过F2作x轴垂直的直线交椭圆C于A、B两点,△F1AB的面积为3,抛物线E:y2=2px(p>0)以椭圆C的右焦点F2为焦点.
椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的左、右焦点分别为F1,F2,离心率e=$\frac{1}{2}$,过F2作x轴垂直的直线交椭圆C于A、B两点,△F1AB的面积为3,抛物线E:y2=2px(p>0)以椭圆C的右焦点F2为焦点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com