
【题目】若以连续掷两次骰子分别得到的点数m、n作为点P的坐标(m,n),求:
(1)点P在直线x+y=7上的概率;
(2)点P在圆x2+y2=25外的概率.
(3)将m,n,5的值分别作为三条线段的长,求这三条线段能围成等腰三角形的概率.
【答案】
(1)解:列表如下;
1 | 2 | 3 | 4 | 5 | 6 | |
1 | 2 | 3 | 4 | 5 | 6 | 7 |
2 | 3 | 4 | 5 | 6 | 7 | 8 |
3 | 4 | 5 | 6 | 7 | 8 | 9 |
4 | 5 | 6 | 7 | 8 | 9 | 10 |
5 | 6 | 7 | 8 | 9 | 10 | 11 |
6 | 7 | 8 | 9 | 10 | 11 | 12 |
由上表格可知,所有的点P坐标(m,n)共计36个,其中满足x+y=7的有6个,
所以P点在直线x+y=7上的概率为 ![]() =
= ![]() ;
;
(2)解:在圆x2+y2=25内的点P有(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),
(2,3),(2,4)(3,1),(3,2),(3,3),(4,1),(4,2),共计13个,
在圆上的点P有(3,4),(4,3),共计2个,
上述共有15个点在圆内或圆上,可得点P在圆x2+y2=25外的概率为
1﹣ ![]() =
= ![]() ;
;
(3)解:当m=n时,它们可以都等于3、4、5、6,共计4种;
当m=5时,n=1,2,3,4,6,共计5种;
n=5时,m=1,2,3,4,6,共计5种.
综上,这三条线段能围成等腰三角形的共有4+5+5=14种.
而所有的情况共有6×6=36种,
∴这三条线段能围成等腰三角形的概率为P= ![]() =
= ![]()
【解析】(1)列格可知,所有的点P坐标(m,n)共计36个,其中满足x+y=7的有6个,由此求得P点在直线x+y=7上的概率.(2)用列举法求得在圆x2+y2=25内的点P13个,在圆上的点P有2个,可得共有15个点在圆内或圆外,用1减去点在圆内或圆上的概率,即得所求;(3)分类讨论求得这三条线段能围成等腰三角形的共有14种,而所有的情况共有6×6=36种,由此可得这三条线段能围成等腰三角形的概率.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:高中数学 来源: 题型:
【题目】某地区有云龙山,户部山,子房山河九里山等四大名山,一位游客来该地区游览,已知该游客游览云龙山的概率为![]() ,游览户部山、子房山和九里山的概率都是
,游览户部山、子房山和九里山的概率都是![]() ,且该游客是否游览这四座山相互独立.
,且该游客是否游览这四座山相互独立.
(1)求该游客至少游览一座山的概率;
(2)用随机变量![]() 表示该游客游览的山数,求
表示该游客游览的山数,求![]() 的概率分布和数学期望
的概率分布和数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:y2=2px(p>0)的焦点为F,过F作垂直于x轴的直线交抛物线于A,B,两点,△AOB的面积为8,直线l与抛物线C相切于Q点,P是l上一点(不与Q重合). 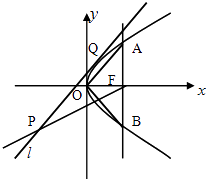
(1)求抛物线C的方程;
(2)若以线段PQ为直径的圆恰好经过F,求|PF|的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设圆![]() 满足:(1)截
满足:(1)截![]() 轴所得弦长为2;(2)被
轴所得弦长为2;(2)被![]() 轴分成两段圆弧,其弧长的比为
轴分成两段圆弧,其弧长的比为![]() .在满足条件(1)、(2)的所有圆中,圆心到直线
.在满足条件(1)、(2)的所有圆中,圆心到直线![]() 的距离最小的圆的方程为__________.
的距离最小的圆的方程为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在棱长为2的正方体ABCD﹣A1B1C1D1中,点P是正方体棱上的一点(不包括棱的端点),满足|PB|+|PD1|= ![]() 的点P的个数为;若满足|PB|+|PD1|=m的点P的个数为6,则m的取值范围是 .
的点P的个数为;若满足|PB|+|PD1|=m的点P的个数为6,则m的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以原点为极点,
为参数),以原点为极点, ![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
![]() 写出曲线
写出曲线![]() 的极坐标的方程以及曲线
的极坐标的方程以及曲线![]() 的直角坐标方程;
的直角坐标方程;
![]() 若过点
若过点![]() (极坐标)且倾斜角为
(极坐标)且倾斜角为![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
, ![]() 两点,弦
两点,弦![]() 的中点为
的中点为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
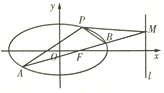
【题目】如图,椭圆![]() 经过点
经过点![]() ,离心率
,离心率![]() ,直线
,直线![]() 的方程为
的方程为![]() .
.
![]() 求椭圆
求椭圆![]() 的方程;
的方程;
![]()
![]() 是经过右焦点
是经过右焦点![]() 的任一弦(不经过点
的任一弦(不经过点![]() ),设直线
),设直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,记
,记![]() ,
, ![]() ,
, ![]() 的斜率为
的斜率为![]() ,
, ![]() ,
, ![]() .问:是否存在常数
.问:是否存在常数![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com