
【题目】设圆![]() 满足:(1)截
满足:(1)截![]() 轴所得弦长为2;(2)被
轴所得弦长为2;(2)被![]() 轴分成两段圆弧,其弧长的比为
轴分成两段圆弧,其弧长的比为![]() .在满足条件(1)、(2)的所有圆中,圆心到直线
.在满足条件(1)、(2)的所有圆中,圆心到直线![]() 的距离最小的圆的方程为__________.
的距离最小的圆的方程为__________.
【答案】![]() 或
或![]()
【解析】设圆的圆心为P(a,b),半径为r,则点P到x轴,y轴的距离分别为|b|,|a|.
由题设知圆P截x轴所得劣弧对的圆心角为90°,知圆P截X轴所得的弦长为![]() ,故r2=2b2,又圆P截y轴所得的弦长为2,所以有r2=a2+1.
,故r2=2b2,又圆P截y轴所得的弦长为2,所以有r2=a2+1.
从而得2b2﹣a2=1.又点P(a,b)到直线x﹣2y=0的距离为![]() ,
,
所以5d2=|a﹣2b|2=a2+4b2﹣4ab≥a2+4b2﹣2(a2+b2)=2b2﹣a2=1,
当且仅当a=b时上式等号成立,此时5d2=1,从而d取得最小值.
由此有![]() ,解此方程组得
,解此方程组得![]() 或
或![]() 由于r2=2b2知
由于r2=2b2知![]() .
.
于是,所求圆的方程是(x﹣1)2+(y﹣1)2=2,或(x+1)2+(y+1)2=2.
解法二:同解法一,得![]()
∴![]() ,得
,得![]() ①
①
将a2=2b2﹣1代入①式,整理得![]() ②
②
把它看作b的二次方程,由于方程有实根,故判别式非负,即
△=8(5d2﹣1)≥0,得5d2≥1.∴5d2有最小值1,从而d有最小值![]() .
.
将其代入②式得2b2±4b+2=0.解得b=±1.
将b=±1代入r2=2b2,得r2=2.由r2=a2+1得a=±1.
综上a=±1,b=±1,r2=2.由|a﹣2b|=1知a,b同号.
于是,所求圆的方程是(x﹣1)2+(y﹣1)2=2,或(x+1)2+(y+1)2=2.


科目:高中数学 来源: 题型:
【题目】设二次函数f(x)=x2+bx+c(b,c∈R),f(1)=0,且1≤x≤3时,f(x)≤0恒成立,f(x)是区间[2,+∞)上的增函数.函数f(x)的解析式是;若|f(m)|=|f(n)|,且m<n<2,u=m+n,u的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等比数列{an}的各项均为正数,且2a1+3a2=1,a32=9a2a6 .
(1)求数列{an}的通项公式;
(2)设bn=|10+2log3an|,求数列{bn}的前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若以连续掷两次骰子分别得到的点数m、n作为点P的坐标(m,n),求:
(1)点P在直线x+y=7上的概率;
(2)点P在圆x2+y2=25外的概率.
(3)将m,n,5的值分别作为三条线段的长,求这三条线段能围成等腰三角形的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆M:x2+(y﹣4)2=4,点P是直线l:x﹣2y=0上的一动点,过点P作圆M的切线PA、PB,切点为A、B.
(1)当切线PA的长度为2 ![]() 时,求点P的坐标;
时,求点P的坐标;
(2)若△PAM的外接圆为圆N,试问:当P运动时,圆N是否过定点?若存在,求出所有的定点的坐标;若不存在,说明理由;
(3)求线段AB长度的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的圆锥中,OP是圆锥的高,AB是底面圆的直径,点C是弧AB的中点,E是线段AC的中点,D是线段PB的中点,且PO=2,OB=1. 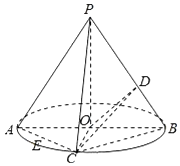
(1)试在PB上确定一点F,使得EF∥面COD,并说明理由;
(2)求点A到面COD的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com