Question

10．如图，已知小矩形蓄水池ABCD中，AB=3米，AD=2米，现要将小矩形蓄水池扩建为大矩形蓄水池AEPF，使点B在AE上，点D在AF上，且对角线EF过点C．
（1）分别求矩形AEPF的面积和周长的最小值及对应AE的长；
（2）求|CF|•|CE|的最小值及此时AE的长．

Answer 1

分析 以A为原点建立平面直角坐标系，设E（a，0），F（0，b），则直线EF方程为$\frac{x}{a}$+$\frac{y}{b}$=1，得出$\frac{3}{a}+\frac{2}{b}$=1．
（1）分别求矩形AEPF的面积和周长，利用基本不等式，即可求出最小值及对应AE的长；
（2）利用|CF|•|CE|=-$\overrightarrow{CF}$$•\overrightarrow{CE}$，即可求|CF|•|CE|的最小值及此时AE的长．

解答 解：以A为原点建立平面直角坐标系，设E（a，0），F（0，b），则直线EF方程为$\frac{x}{a}$+$\frac{y}{b}$=1，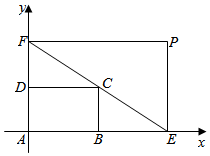

∵EF过点C，∴$\frac{3}{a}+\frac{2}{b}$=1．
（1）矩形AEPF的面积S=ab，1=$\frac{3}{a}+\frac{2}{b}$≥$2\sqrt{\frac{6}{ab}}$，
∴ab≥24，当且仅当$\frac{3}{a}=\frac{2}{b}$，即a=6，b=4时等号成立；
周长l=2（a+b）=2（a+b）（$\frac{3}{a}+\frac{2}{b}$）=2（5+$\frac{3b}{a}$+$\frac{2a}{b}$）≥2（5+2$\sqrt{6}$），
当且仅当$\frac{3b}{a}$=$\frac{2a}{b}$，即a=3+$\sqrt{6}$时等号成立；
（2）∵$\overrightarrow{CF}$$•\overrightarrow{CE}$=-|CF|•|CE|，
∴|CF|•|CE|=-$\overrightarrow{CF}$$•\overrightarrow{CE}$=-（-3，b-2）•（a-3，-2）=3a+2b-13=（3a+2b）（$\frac{3}{a}+\frac{2}{b}$）-13=$\frac{6b}{a}+\frac{6a}{b}$≥12，
当且仅当a=b，即a=5时等号成立，
∴|CF|•|CE|的最小值为12，此时AE=5．

点评 本题考查基本不等式的运用，考查利用数学知识解决实际问题，考查学生分析解决问题的能力，属于中档题．