
分析 由α为第三象限的角,判断出2α可能的范围,再结合又cos2α=-$\frac{3}{5}$<0确定出2α在第二象限,利用同角三角函数关系求出其正弦,再由两角和的正切公式展开代入求值.
解答 解:因为:α为第三象限的角,
所以:2α∈(2(2k+1)π,π+2(2k+1)π)(k∈Z),
又cos2α=-$\frac{3}{5}$<0,
所以:2α∈($\frac{π}{2}$+2(2k+1)π,π+2(2k+1)π)(k∈Z),
于是:有sin2α=$\frac{4}{5}$,tan2α=$\frac{sin2α}{cos2α}$=-$\frac{4}{3}$,
所以:tan(π-2α)=-tan2α=$\frac{4}{3}$.
故答案为:$\frac{4}{3}$.
点评 本小题主要考查三角函数值符号的判断、同角三角函数关系、和角的正切公式,同时考查了基本运算能力及等价变换的解题技能,属于中档题.


 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
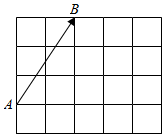 如图,在4×5的方格纸中有一个向量$\overrightarrow{AB}$(每个小方格都是单位小正方形),分别以图中的格点为起点和终点作向量,其中与$\overrightarrow{AB}$相等的向量有7个,与$\overrightarrow{AB}$相反的向量有8个;与$\overrightarrow{AB}$长度相等的共线向量有15个($\overrightarrow{AB}$除外);与$\overrightarrow{AB}$方向相同且模为5的向量有3个.
如图,在4×5的方格纸中有一个向量$\overrightarrow{AB}$(每个小方格都是单位小正方形),分别以图中的格点为起点和终点作向量,其中与$\overrightarrow{AB}$相等的向量有7个,与$\overrightarrow{AB}$相反的向量有8个;与$\overrightarrow{AB}$长度相等的共线向量有15个($\overrightarrow{AB}$除外);与$\overrightarrow{AB}$方向相同且模为5的向量有3个.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({\sqrt{2},+∞})$ | B. | $({\sqrt{2},2})$ | C. | $({2,2+\sqrt{2}})$ | D. | $({\sqrt{5},+∞})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3n(2n-1) | B. | 3n(2n+1) | C. | $\frac{3n(n+1)}{2}$ | D. | $\frac{3n(n-1)}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com