
| A. | $({\sqrt{2},+∞})$ | B. | $({\sqrt{2},2})$ | C. | $({2,2+\sqrt{2}})$ | D. | $({\sqrt{5},+∞})$ |
分析 由正方形的对称性得,其对称中心在原点,且在第一象限的顶点坐标为(x,x),从而得到双曲线渐近线的斜率k=$\frac{b}{a}$>1,由此能求出双曲线离心率的取值范围.
解答 解:∵双曲线M上存在四个点A,B,C,D,使得四边形ABCD是正方形,
∴由正方形的对称性得,其对称中心在原点,
且在第一象限的顶点坐标为(x,x),
∴双曲线渐近线的斜率k=$\frac{b}{a}$>1,
∴双曲线离心率e=$\sqrt{1+(\frac{b}{a})^{2}}$>$\sqrt{2}$.
∴双曲线M的离心率的取值范围是($\sqrt{2}$,+∞).
故选:A.
点评 本题考查双曲线的离心率的取值的范围的求法,是中档题,解题时要认真审题,注意双曲线性质的合理运用.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:高中数学 来源: 题型:选择题
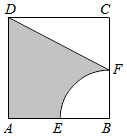 如图所示,在边长为2的正方形ABCD中,圆心为B,半径为1的圆与AB、BC分别交于E,F,则阴影部分绕直线BC旋转一周形成几何体的体积等于( )
如图所示,在边长为2的正方形ABCD中,圆心为B,半径为1的圆与AB、BC分别交于E,F,则阴影部分绕直线BC旋转一周形成几何体的体积等于( )| A. | π | B. | 6π | C. | $\frac{4π}{3}$ | D. | 4π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | p∨(¬q) | C. | (¬p)∨q | D. | ¬(p∨q) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
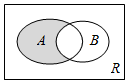
| A. | (-4,1] | B. | (1,2) | C. | [1,2) | D. | (-4,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1,2} | B. | {-2,-1} | C. | {-2,-1,0} | D. | {1,2,0} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com