
分析 (1)利用递推式与等比数列的通项公式即可得出;
(2)bn=nan=2n×4n-1,利用“错位相减法”、等比数列的前n项和公式即可得出.
(3)不等式Tn+$\frac{a}{n}$•22n+1-$\frac{2}{9}$>0的n∈N*恒成立,化为a>$\frac{n(2-6n)}{36}$,利用二次函数的单调性即可得出.
解答 解:(1)∵an=$\frac{3}{4}$Sn+$\frac{1}{2}$(n∈N*),∴当n=1时,${a}_{1}=\frac{3}{4}{a}_{1}+\frac{1}{2}$,解得a1=2.
当n≥2时,${a}_{n-1}=\frac{3}{4}{S}_{n-1}+\frac{1}{2}$,∴an-an-1=$\frac{3}{4}{a}_{n}$,∴an=4an-1,
∴数列{an}是等比数列,首项为2,公比为4,
∴${a}_{n}=2×{4}^{n-1}$.
(2)bn=nan=2n×4n-1,
∴数列{bn}的前n项和Tn=2(1+2×4+3×42+…+n×4n-1),
∴4Tn=2(4+2×42+3×43+…+n×4n),
∴-3Tn=2(1+4+42+…+4n-1-n×4n)=2$(\frac{{4}^{n}-1}{4-1}-n×{4}^{n})$,
∴Tn=$\frac{(6n-2)×{4}^{n}+2}{9}$.
(3)不等式Tn+$\frac{a}{n}$•22n+1-$\frac{2}{9}$>0的n∈N*恒成立,∴$\frac{(6n-2)×{4}^{n}+2}{9}$+$\frac{a}{n}$•22n+1-$\frac{2}{9}$>0,
化为a>$\frac{n(1-3n)}{9}$,
∵$\frac{n(1-3n)}{9}$=$-\frac{1}{3}(n-\frac{1}{6})^{2}$+$\frac{1}{108}$≤-$\frac{2}{9}$,(n=1时)
∴a>$\frac{2}{9}$.
∴实数a的取值范围是$(-\frac{2}{9},+∞)$.
点评 本题考查了递推式与等比数列的通项公式及其前n项和公式、“错位相减法”、恒成立问题的等价转化方法、二次函数的单调性,考查了推理能力与计算能力,属于中档题.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在平面直角坐标系xOy中,A和B分别是椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)和
如图,在平面直角坐标系xOy中,A和B分别是椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)和查看答案和解析>>
科目:高中数学 来源: 题型:选择题
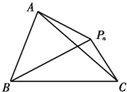 如图,△ABC所在平面上的点Pn(n∈N*)均满足△PnAB与△PnAC的面积比为3:1,$\overrightarrow{{P_n}A}$=$\frac{{{x_{n+1}}}}{3}$$\overrightarrow{{P_n}B}$-(2xn+1)$\overrightarrow{{P_n}C}$(其中,{xn}是首项为1的正项数列),则x4等于( )
如图,△ABC所在平面上的点Pn(n∈N*)均满足△PnAB与△PnAC的面积比为3:1,$\overrightarrow{{P_n}A}$=$\frac{{{x_{n+1}}}}{3}$$\overrightarrow{{P_n}B}$-(2xn+1)$\overrightarrow{{P_n}C}$(其中,{xn}是首项为1的正项数列),则x4等于( )| A. | 15 | B. | 17 | C. | 33 | D. | 31 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$ | B. | 1 | C. | $\frac{9}{2}$ | D. | -$\frac{9}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 对任意的x∈R,x2<0 | B. | 不存在x∈R,x2<0 | ||
| C. | 存在x∈R,x2<0 | D. | 存在x∈R,x2≥0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com