
| A. | $\frac{x^2}{4}-\frac{y^2}{5}=1$ | B. | $\frac{y^2}{5}-\frac{x^2}{4}=1$ | C. | $\frac{x^2}{4}-\frac{y^2}{5}=1$(x≤-2) | D. | $\frac{y^2}{5}-\frac{x^2}{4}=1$(y$≤-\sqrt{5}$) |
分析 根据题意,分析根式$\sqrt{(x-3)^{2}+{y}^{2}}$和$\sqrt{(x+3)^{2}+{y}^{2}}$的几何意义,可得方程$\sqrt{{{({x-3})}^2}+{y^2}}-\sqrt{{{({x+3})}^2}+{y^2}}=4$表示|PF2|-|PF1|=4的点的轨迹,由双曲线的定义分析可得P的轨迹是以F1(-3,0),F2(3,0)为焦点,且2a=4的双曲线的左支,结合题意求出双曲线的标准方程,即可得答案.
解答 解:根据题意,根式$\sqrt{(x-3)^{2}+{y}^{2}}$表示点(x,y)与点(3,0)之间的距离,
根式$\sqrt{(x+3)^{2}+{y}^{2}}$表示点(x,y)与点(-3,0)之间的距离,
设P(x,y),F1(-3,0),F2(3,0),则|F1F2|=6,
则方程$\sqrt{{{({x-3})}^2}+{y^2}}-\sqrt{{{({x+3})}^2}+{y^2}}=4$表示|PF2|-|PF1|=4的点的轨迹,
则P的轨迹是以F1(-3,0),F2(3,0)为焦点,且2a=4的双曲线的左支,
其中b=$\sqrt{{c}^{2}-{a}^{2}}$=5,
则其方程为:$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{5}$=1(x≤-2);
即方程$\sqrt{{{({x-3})}^2}+{y^2}}-\sqrt{{{({x+3})}^2}+{y^2}}=4$化简的结果为$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{5}$=1(x≤-2);
故选:C.
点评 本题考查双曲线的定义,关键是分析题目中根式的意义,进而结合双曲线的定义进行分析.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $\sqrt{2}$ | C. | $\frac{2}{3}\sqrt{3}$ | D. | $\frac{4}{3}\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若a>b,则ac>bc | B. | 若a2>b2,则a>b>0 | ||
| C. | 若|x-3|>1,则2<x<4 | D. | 若|x2-3|>1,则$\sqrt{2}<x<2$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 大前提错误 | B. | 小前提错误 | C. | 推理形式错误 | D. | 没有错误 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
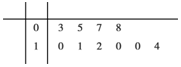 学校举行班级篮球赛,某名运动员每场比赛得分记录的茎叶图如下:
学校举行班级篮球赛,某名运动员每场比赛得分记录的茎叶图如下:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com