
| A. | 大前提错误 | B. | 小前提错误 | C. | 推理形式错误 | D. | 没有错误 |
分析 在使用三段论推理证明中,如果命题是错误的,则可能是“大前提”错误,也可能是“小前提”错误,也可能是推理形式错误,我们分析的其大前提的形式:“对于可导函数f(x),如果f'(x0)=0,那么x=x0是函数f(x)的极值点”,不难得到结论.
解答 解:对于可导函数f(x),如果f'(x0)=0,且满足当x>x0时和当x<x0时的导函数值异号时,那么x=x0是函数f(x)的极值点,
而大前提是:“对于可导函数f(x),如果f'(x0)=0,那么x=x0是函数f(x)的极值点”,不是真命题,
∴大前提错误,
故选:A.
点评 本题考查的知识点是演绎推理的基本方法,演绎推理是一种必然性推理,演绎推理的前提与结论之间有蕴涵关系.因而,只要前提是真实的,推理的形式是正确的,那么结论必定是真实的,但错误的前提可能导致错误的结论.


科目:高中数学 来源: 题型:解答题
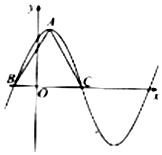 函数f(x)=6cos2$\frac{ωx}{2}$+$\sqrt{3}$sinωx-3(ω>0)在一个周期内的图象如图所示,A为图象的最高点,B,C为图象与x轴的交点,且△ABC为正三角形.
函数f(x)=6cos2$\frac{ωx}{2}$+$\sqrt{3}$sinωx-3(ω>0)在一个周期内的图象如图所示,A为图象的最高点,B,C为图象与x轴的交点,且△ABC为正三角形.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | $\sqrt{7}$ | C. | $4\sqrt{7}$ | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{4}-\frac{y^2}{5}=1$ | B. | $\frac{y^2}{5}-\frac{x^2}{4}=1$ | C. | $\frac{x^2}{4}-\frac{y^2}{5}=1$(x≤-2) | D. | $\frac{y^2}{5}-\frac{x^2}{4}=1$(y$≤-\sqrt{5}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-$\frac{1}{4}$e3,0) | B. | [-$\frac{1}{2}$e,0) | C. | [-$\frac{1}{4}$e3,$\frac{e}{2}$) | D. | [-$\frac{1}{4}$e3,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com