
已知各项均为正数的等差数列 满足:
满足: ,各项均为正数的等比数列
,各项均为正数的等比数列 满足:
满足: ,
, .
.
(1)求数列 和
和 的通项公式;
的通项公式;
(2)若数列 满足:
满足: ,其前
,其前 项和为
项和为 ,证明
,证明 .
.
(1)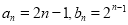 ;(2)见解析
;(2)见解析
【解析】
试题分析:(1)设出等差数列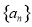 的公差为d,等比数列
的公差为d,等比数列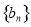 的公比为q,根据已知条件及等差数列和等比数列的通项公式列出关于
的公比为q,根据已知条件及等差数列和等比数列的通项公式列出关于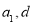 ,
,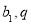 ,通过解方程组解出
,通过解方程组解出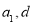 ,
,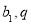 ,即可根据等差数列、等比数列通项公式写出数列
,即可根据等差数列、等比数列通项公式写出数列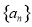 ,
,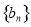 的通项公式;(2)由(1)知数列
的通项公式;(2)由(1)知数列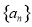 与数列
与数列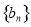 的通项公式,即可求出
的通项公式,即可求出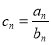 的通项公式,由通项公式知,数列
的通项公式,由通项公式知,数列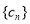 是等差数列与等比数列对应项的乘积构成的数列,其和用错位相减法.
是等差数列与等比数列对应项的乘积构成的数列,其和用错位相减法.
试题解析:(1)设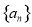 的公差为
的公差为 ,
,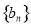 的公比为
的公比为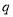 ,则依题意有
,则依题意有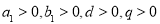
 解得
解得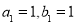 ,
,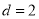 ,
,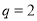 . 4分
. 4分
所以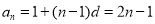 ,
, . 6分
. 6分
(2)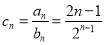 . 7分
. 7分
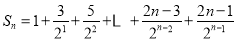 ,①
,①
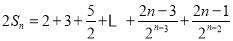 ,②
,②
②-①得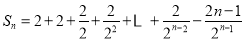 ,
,
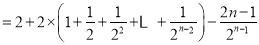

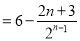
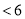 11分
11分
又因为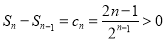 ,所以
,所以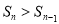 ,所以
,所以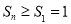 13分
13分
综上 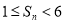 得证. 14分
得证. 14分
考点: 等比数列通项公式;等差数列通项公式;错位相减法;方程思想


 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:高中数学 来源:2015届山西省忻州市高二下学期期中联考理科数学试卷(解析版) 题型:选择题
若直角坐标平面内的两点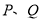 满足条件:①
满足条件:①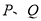 都在函数
都在函数 的图像上;②
的图像上;②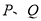 关于原点对称,则称点对
关于原点对称,则称点对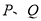 是函数
是函数 的一对“友好点对”(注:点对
的一对“友好点对”(注:点对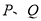 与
与 看作同一对“友好点对”).已知函数
看作同一对“友好点对”).已知函数 ,则此函数的“友好点对”有( )
,则此函数的“友好点对”有( )
A. 0对 B. 1对 C. 2对 D. 3对
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com