分析:(1)以A为坐标原点,AB,AD,AA
1方向分别为x,y,z轴正方向建立空间坐标系,求出平面AB
1D
1的法向量
,则C
1到平面AB
1D
1的距离
d=,代入即可求出点C
1到平面AB
1D
1的距离;
(2)求出平面CDD
1C
1的一个法向量
,结合(1)中平面AB
1D
1的法向量
,代入向量夹角公式,即可求出二面角的平面角的余弦值,进而得到平面CDD
1C
1与平面AB
1D
1所成的二面角的大小.
解答: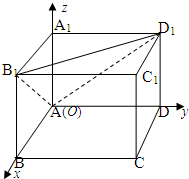
解:(1)按如图所示建立空间直角坐标系,可得有关点的坐标为A(0,0,0)、D
1(0,a,a)、B
1(a,0,a)、C
1(a,a,a)
,向量
=(-a,-a,-a),
=(0,a,a),
=(a,0,a)设
=(x,y,z)是平面AB
1D
1的法向量,于是,有
,
即
.
令z=-1,得x=1,y=1.
于是平面AB
1D
1的一个法向量是
=(1,1,-1).(5分)
因此,C
1到平面AB
1D
1的距离
d==a(8分)
(2)由(1)知,平面AB
1D
1的一个法向量是
=(1,1,-1).又因AD⊥平面CDD
1C
1,故平面CDD
1C
1的一个法向量是
=(0,1,0).(10分)
设所求二面角的平面角为θ,则
cosθ==.(13分)
所以,平面CDD
1C
1与平面AB
1D
1所成的二面角为
arccos.(14分)
点评:本题考查的知识点是用空间向量求平面间的夹角,点到平面的距离,其中(1)的关键是求出平面AB
1D
1的法向量
,然后代入
d=中求解,(2)的关键是求出平面CDD
1C
1的一个法向量
和平面AB
1D
1的法向量
,将二面角问题转化为向量夹角问题.

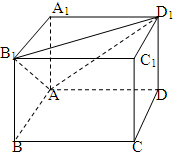 已知正方体ABCD-A1B1C1D1的棱长为a.
已知正方体ABCD-A1B1C1D1的棱长为a. 解:(1)按如图所示建立空间直角坐标系,可得有关点的坐标为A(0,0,0)、D1(0,a,a)、B1(a,0,a)、C1(a,a,a)
解:(1)按如图所示建立空间直角坐标系,可得有关点的坐标为A(0,0,0)、D1(0,a,a)、B1(a,0,a)、C1(a,a,a)

 如图,已知正方体ABCD-A1B1C1D1的棱长为2,点P在平面DD1C1C内,PD1=PC1=
如图,已知正方体ABCD-A1B1C1D1的棱长为2,点P在平面DD1C1C内,PD1=PC1=