练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    19．用反证法证明命题：“已知x∈R，a=x2-1，b=2x+2，则a，b中至少有一个不小于0”，反设正确的是（　　）
    A．假设a，b都不大于0B．假设a，b至多有一个大于0
    C．假设a，b都大于0D．假设a，b都小于0

    分析 根据用反证法证明数学命题的方法和步骤，应先假设命题的否定成立，而要证明题的否定为：“假设a，b都小于0”，从而得出结论．

    解答 解：根据用反证法证明数学命题的方法和步骤，应先假设命题的否定成立，
    而命题：“已知x∈R，a=x2-1，b=2x+2，则a，b中至少有一个不小于0”的否定为“假设a，b都小于0”，
    故选：D．

    点评 本题主要考查用命题的否定，反证法证明数学命题的方法和步骤，把要证的结论进行否定，得到要证的结论的反面，是解题的突破口，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

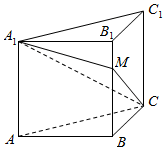    9．棱长为1的正方体ABCD-A1B1C1D1中，沿平面A1ACC1将正方体分成两部分，其中一部分如图所示，过直线A1C的平面A1CM与线段BB1交于点M．
    （Ⅰ）当M与B1重合时，求证：MC⊥AC1；
    （Ⅱ）当平面A1CM⊥平面A1ACC1时，求平面A1CM分几何体所得两部分体积之比．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    10．已知数列{an}对任意p，q∈N+满足ap+q=ap+aq，且a2=-6，那么a4=-12．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

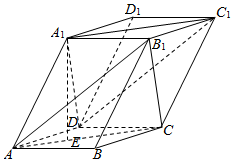    7．如图，棱柱ABCD-A1B1C1D1的底面是菱形．侧棱长为5，平面ABCD⊥平面A1ACC1，AB=3$\sqrt{3}$，∠BAD=60°，点E是△ABD的重心，且A1E=4．
    （1）求证：平面A1DC1∥平面AB1C；
    （2）求棱柱ABCD-A1B1C1D1的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    14．已知tan（α+β）=$\frac{3}{5}$，tanα=$\frac{1}{3}$，则tan（β+$\frac{π}{4}$）的值为$\frac{11}{7}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．省农科所经过5年对甲、乙两棉种的实验研究，将连续5年棉花产量（千克/亩）的统计数据用茎叶图表示如图，则平均产量较高与产量较稳定的分别是（　　）
    A．棉农甲；棉农甲B．棉农乙；棉农甲C．棉农甲；棉农乙D．棉农乙；棉农乙

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．函数f（x）的图象如图所示，则f（x）的极大值点的个数为（　　）
    A．0B．1C．2D．3

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．已知复数z满足（1-i）z=2（i为虚数单位），则（　　）
    A．|z|=2B．z的实部为1
    C．z的虚部为-1D．z的共轭复数为1+i

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．已知F、A分别为双曲线$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1（a＞0，b＞0）的右焦点和右顶点，过F作x轴的垂线在第一象限与双曲线交于点P，AP的延长线与双曲线在第一象限的渐近线交于点Q，若$\overrightarrow{AP}$=（2-$\sqrt{2}}$）$\overrightarrow{AQ}$，则双曲线的离心率为（　　）
    A．$\sqrt{2}$B．$\sqrt{3}$C．2$\sqrt{2}$D．$\sqrt{5}$

    查看答案和解析>>

    同步练习册答案