
| 期末分数段 | (0,60) | [60,75) | [75,90) | [90,105) | [105,120) | [120,150] |
| 人数 | 5 | 10 | 15 | 10 | 5 | 5 |
| “过关”人数 | 1 | 2 | 9 | 7 | 3 | 4 |
| 分数低于90分人数 | 分数不低于90分人数 | 合计 | |
| 过关人数 | 12 | 14 | 26 |
| 不过关人数 | 18 | 6 | 24 |
| 合计 | 30 | 20 | 50 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 |
| k | 2.072 | 2.706 | 3.841 | 5.024 |
分析 (1)依题意求出a、b、c、d的值,填写列联表;计算观测值K2,对照数表得出概率结论;
(2)求出在期末分数段[105,120)的5人中随机选3人,“过关”人数X的分布列与数学期望值.
解答 解:(1)依题意得,a=12,b=18,c=14,d=6,
填写列联表如下;
| 分数低于9(0分)人数 | 分数高于9(0分)人数 | 合计 | |
| 过关人数 | 12 | 14 | 26 |
| 不过关人数 | 18 | 6 | 24 |
| 合计 | 30 | 20 | 50 |
| X | 1 | 2 | 3 |
| P | $\frac{3}{10}$ | $\frac{6}{10}$ | $\frac{1}{10}$ |
点评 本题考查了离散型随机变量的分布列与数学期望的应用问题,也考查了独立性检验的应用问题,是综合性题目.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=x,$g(x)=\sqrt{x{\;}^2}$ | B. | f(x)=x,$g(x)=\root{3}{x^3}$ | ||
| C. | f(x)=sinx,g(x)=sin(π+x) | D. | f(x)=x,g(x)=elnx |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
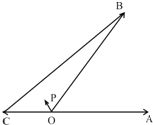 如图:已知$\overrightarrow{OC}=-\frac{1}{2}\overrightarrow{OA}$,若$\overrightarrow{OP}$的终点P在△OBC的边界及内部,且$\overrightarrow{OP}=x\overrightarrow{OA}+y\overrightarrow{OB}$则x、y满足的条件为( )
如图:已知$\overrightarrow{OC}=-\frac{1}{2}\overrightarrow{OA}$,若$\overrightarrow{OP}$的终点P在△OBC的边界及内部,且$\overrightarrow{OP}=x\overrightarrow{OA}+y\overrightarrow{OB}$则x、y满足的条件为( )| A. | $\left\{{\begin{array}{l}{-\frac{1}{2}≤x≤0}\\{0≤y≤1}\end{array}}\right.$ | B. | $\left\{{\begin{array}{l}{x≤0}\\{y≥0}\\{y-2x-1≤0}\end{array}}\right.$ | ||
| C. | $\left\{{\begin{array}{l}{x≤0}\\{y≥0}\\{2y-x-1≤0}\end{array}}\right.$ | D. | $\left\{{\begin{array}{l}{-\frac{1}{2}≤x≤0}\\{0≤y≤1}\\{y-2x-1≤0}\end{array}}\right.$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 7,-20 | B. | 0,-9 | C. | -9,-20 | D. | -4,-20 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | -4 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ②③ | C. | ①②③ | D. | ①②④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com