
分析 (1)求出f′(x),令f′(x)>0,f′(x)<0解出f(x)的单调区间;
(2)判断f(x)的单调性,求出f(x)的最小值fmin(x),令fmin(x)>$\frac{1}{2}$(e+1)a解出a的范围.
解答 解:(1)a=-1时,f(x)=x2-x-lnx,
f′(x)=2x-1-$\frac{1}{x}$=$\frac{2{x}^{2}-x-1}{x}$.
令f′(x)=0得x=-$\frac{1}{2}$(舍)或x=1.
∴当0<x<1时,f′(x)<0,当x>1时,f′(x)>0.
∴f(x)的单调增区间为(1,+∞),单调减区间为(0,1).
(2)f′(x)=2x+a+$\frac{a}{x}$=$\frac{2{x}^{2}+ax+a}{x}$.
令f′(x)=0得x=$\frac{-a+\sqrt{{a}^{2}-8a}}{4}$或x=$\frac{-a-\sqrt{{a}^{2}-8a}}{4}$(舍).
∴当0<x<$\frac{-a+\sqrt{{a}^{2}-8a}}{4}$时,f′(x)<0,当x>$\frac{-a+\sqrt{{a}^{2}-8a}}{4}$时,f′(x)>0.
∴f(x)在(0,$\frac{-a+\sqrt{{a}^{2}-8a}}{4}$)上单调递减,在($\frac{-a+\sqrt{{a}^{2}-8a}}{4}$,+∞)上单调递增.
∴fmin(x)=f($\frac{-a+\sqrt{{a}^{2}-8a}}{4}$).
设$\frac{-a+\sqrt{{a}^{2}-8a}}{4}$=t,则2t2+at+a=0,∴t2=$\frac{-at-a}{2}$.
∴f($\frac{-a+\sqrt{{a}^{2}-8a}}{4}$)=f(t)=t2+at+alnt=$\frac{-at-a}{2}$+at+alnt=$\frac{1}{2}$at-$\frac{1}{2}$a+alnt.
∵f(x)>$\frac{1}{2}$(e+1)a,∴$\frac{1}{2}$at-$\frac{1}{2}$a+alnt>$\frac{1}{2}$(e+1)a,
∵a<0,∴$\frac{1}{2}$t+lnt<$\frac{e}{2}$+1,∴t<e.
即0<$\frac{-a+\sqrt{{a}^{2}-8a}}{4}$<e,解得-$\frac{2{e}^{2}}{e+1}$<a<0.
点评 本题考查了导数与函数单调性的关系,函数最值的计算,属于中档题.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x大大增大,y一定变大,z可能不变 | B. | x可能不变,y可能不变,z可能不变 | ||
| C. | x大大增大,y可能不变,z也不变 | D. | x大大增大,y可能不变,z变大 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
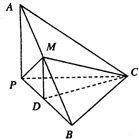 如图,已知三棱锥A-BPC中,AP⊥PC,AC⊥BC,M为AB中点,D为PB中点,且△PMB为正三角形.
如图,已知三棱锥A-BPC中,AP⊥PC,AC⊥BC,M为AB中点,D为PB中点,且△PMB为正三角形.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 45°或135° | B. | 135° | C. | 45° | D. | 以上答案都不对 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com